Türkçe Bilgi logo TürkçeBilgi

Skellam Dağılımı

Kısaca: Skellam dağılımı bir ayrık olasılık dağılım tipidir. Skellam dağılımı iki tane (aralarında korelasyon bulunabilen ve) beklenen değerleri \mu_1 ve \mu_2 olan Poisson dağılımı gösteren rassal değişken K_1 ve K_2 arasında bulunan fark olan K_1-K_2nin gösterdiği olasılık dağılımdır. ...devamı ☟

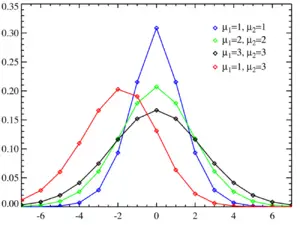
Skellam dağılımı
Skellam Dağılımı

Skellam dağılımı bir ayrık olasılık dağılım tipidir. Skellam dağılımı iki tane (aralarında korelasyon bulunabilen ve) beklenen değerleri \mu_1 ve \mu_2 olan Poisson dağılımı gösteren rassal değişken K_1 ve K_2 arasında bulunan fark olan K_1-K_2nin gösterdiği olasılık dağılımdır. Kullanış alanları çok farklılık göstermektedir; beyzbol, buz hokeyi ve futbol gibi sporlarda ABD'de çok popüler olan yayılmış bahis (spread betting) yöntemini tanımlamak ve fizikte iki imajin basit foton gürültüsünü (photon noise) açıklamak için kullanılmıştır. Karaketeristikler Bu kısımda geliştirilen karakteristikler iki değişkenin arasındaki korelasyonun etkilerini ele almayacaktır. Aralarında korelasyon bulunan iki değişken farkının da analize katılması ile ortaya çıkan sonuçlar için bakın . Önce bir Poisson dağılımı için olasılık kütle fonksiyonunun şu olduğu hatırlansın: : f(k;\mu)=e^\, Skellam olasılık kütle fonksiyonu iki Poisson dağılım arasındaki çapraz korelasyon olur (Skellam, 1946) : f(k;\mu_1,\mu_2) =\sum_^\infty \!f(k\!+\!n;\mu_1)f(n;\mu_2) : =e^\sum_^\infty : = e^ \left(\right)^I_k(2\sqrt) Burada Ik(z) birinci şekilde değiştirilmiş Bessel fonksiyonu olur. Yukarıdaki formüller için eğer faktoriyel negatif değer taşımaktaysa o değerin 0 olacağı kabul edilmiştir. Bir özel hal olan \mu_1=\mu_2(=\mu) için bakin : f\left(k;\mu,\mu\right) = e^I_k(2\mu) Eğer değerler küçükse, Bessel fonksiyonu için limit değerleri kullanılarak, Poisson dağılımını \mu_2=0 için ozel bir hal olarak Skellam dağılımı yerine kullanabiliriz. Özellikler Skellem dağılımı için olasılık kütle dağılımı normalize edilerek şöyle elde edilir: : \sum_^\infty f(k;\mu_1,\mu_2)=1. Poisson dağılımı için olasılık üreten fonksiyon şöyle verilir: : G\left(t;\mu\right)= e^. Bunlar kullanılarak Skellam dağılımı için olasılık üreten fonksiyon ortaya çıkartılır: :G(t;\mu_1,\mu_2) = \sum_^\infty f(k;\mu_1,\mu_2)t^k := G\left(t;\mu_1\right)G\left(1/t;\mu_2\right)\, := e^. Olasılık üreten fonksiyonu incelenince görülmektedir ki herhangi bir sayıda bağımsız Skellam dağılımı gösteren değişkenlerin toplamları veya farklılıkları da tekrar Skellam dağılımı göstereceklerdir. Bazı referanslara gore iki Skellam dağılımlı değişkenin herhangi bir doğrusal bileşiği de Skellem dağılımı gösterir. Fakat bu doğru değildir; çünkü herhangi çarpım sayısı dağılımın destek alanını değiştirecektir. Skellam dağılımı için moment üreten fonksiyon şudur: :M\left(t;\mu_1,\mu_2\right) = G(e^t;\mu_1,\mu_2) : = \sum_^\infty \,m_k Bunlardan ham moment değerleri mk bulmak icin şu tanımlara bakılsın: :\Delta\ \stackrel}\ \mu_1-\mu_2\, :\mu\ \stackrel}\ (\mu_1+\mu_2)/2.\, Bunlardan 3 ham moment mk değerleri şöyle çıkartılır: :m_1=\left.\Delta\right.\, :m_2=\left.2\mu+\Delta^2\right.\, :m_3=\left.\Delta(1+6\mu+\Delta^2)\right.\, Merkezsel momentler M k şunlardır: :M_2=\left.2\mu\right.,\, :M_3=\left.\Delta\right.,\, :M_4=\left.2\mu+12\mu^2\right..\, Beklenen değer, varyans, çarpıklık katsayısı and basıklık katsayısı sırasıyla şöyle verilir:: :\left.\right.E(n)=\Delta\, :\sigma^2=\left.2\mu\right.\, :\gamma_1=\left.\Delta/(2\mu)^\right.\, :\gamma_2=\left.1/2\mu\right..\, Kümülant üreten fonksiyon şu şekilde verilmiştir: : K(t;\mu_1,\mu_2)\ \stackrel}\ \ln(M(t;\mu_1,\mu_2)) = \sum_^\infty \,\kappa_k ve bundan kümülant değerleri elde edilir: :\kappa_=\left.2\mu\right. :\kappa_=\left.\Delta\right. . Özel hal olan μ1 = μ2 için ayrıntılı sonuçlar M.Abromowitz et.al. referansındadır. .

Kaynak

*

Referanslar

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Olasılık dağılımı
2 yıl önce

tanımlar. Skellam dağılımı: İki bağımsız Poisson dağılımı gösteren rassal değişken arasındaki farkın dağılımıdır. Yule-Simon dağılımı Zeta dağılımı Kullanılma...
Poisson dağılımı
2 yıl önce

Poisson dağılımı, (okunuşu: puason dağılımı) olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim...

Poisson dağılımı, Olasılık Dağılımları, İstatistik, Planetmath reference, 1781, 1840, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı
Student'in t dağılımı
2 yıl önce

bilim dallarında t-dağılımı ya da Student'in t dağılımı genel olarak örneklem sayısı veya sayıları küçük ise ve anakütle normal dağılım gösterdiği varsayılırsa...

Student`in t dağılımı, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu, Dublin
Pareto Dağılımı
2 yıl önce

kullanılmıştır. İktisat bilim dalı dışında bu dağılım Bradford dağılımı adı altında da bilinmektedir. Pareto dağılımı iktisat dışında, sosyal bilimler, fen,...
Normal Dağılım
2 yıl önce

Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli...

Normal Dağılım, Karl Friedrich Gauss, Rassal değişken, Yoğunluk fonksiyonu, Hipergeometrik dağılım, Pierre Simon Laplace, Abraham de Moivre
Bernoulli dağılımı
2 yıl önce

ayrık olasılık dağılımıdır. İsmi ilk açıklamayı yapan İsviçreli bilim adamı Jakob Bernoulli anısına verilmiştir. Eğer X Bernoulli dağılımı gösteren bir...

Bernoulli dağılımı, Olasılık Dağılımları, İstatistik, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Beta dağılımı, Binom dağılım, Binom dağılımı, Bozulmuş dağılım
Genelleştirilmiş Pareto Dağılımı
6 yıl önce

Pareto dağılımı ailesi, olasılık kuramı ve istatistik bilim dallarında geliştirilen ve özellikle iktisat incelemelerinde gelir ve servet dağılımı analizi...
Ki-kare dağılımı
2 yıl önce

dallarında ki-kare dağılım (x2 dağılımı) özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur. Bu dağılım, gamma dağılımından...

Ki-kare dağılımı, Matematik, Taslak