Olasılık Kütle Fonksiyonu

Kısaca: olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir fonksiyondur. Olasılık kütle fonksiyonu, olasılık yoğunluk fonksiyonundan farklıdır; çünkü olasılık yoğunluk fonksiyonu yalnızca sürekli rassal değişkenler için tanımlanmış olup doğrudan doğruya olasılık değerini vermezler. Olasılık yoğunluk fonksiyonunun bir belli değer aralığı (yani ''a'' ve ''b'' değerleri aralığı) için integrali alinirsa bu rassal değişkenin belirlenen değer ...devamı ☟

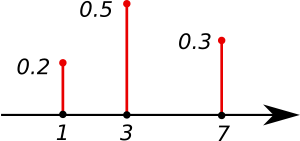
olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir fonksiyondur. Olasılık kütle fonksiyonu, olasılık yoğunluk fonksiyonundan farklıdır; çünkü olasılık yoğunluk fonksiyonu yalnızca sürekli rassal değişkenler için tanımlanmış olup doğrudan doğruya olasılık değerini vermezler. Olasılık yoğunluk fonksiyonunun bir belli değer aralığı (yani a ve b değerleri aralığı) için integrali alinirsa bu rassal değişkenin belirlenen değer aralığı için olasılığını verir. Matematiksel tanımlama Eğer X S ⊆ R örneklem uzayında bazı sayılabilir değerleri alabilen bir ayrık rassal değişken ise, o halde X için verilmiş, f_X(x), olasılık kütle fonksiyonu, şöyle ifade edilir: :

f_X(x) = \begin \Pr(X = x), &x\in S,\\0, &x\in \mathbb\backslash S.\end

Dikkat edilirse bu çok açık bir surette, f_X(x) fonksiyonunu tüm reel sayılar için tanımlamaktadir; ama birçok sayı değerine sıfır olasılık saptanmaktadır. Olasılık kütle fonksiyonlarinda bulunan süreksizlik, bir ayrık rassal değişken için yığmalı dağılım fonksiyonun süreksiz olması gerçeğini yansıtmaktadır. Bu fonksiyonun eğer türevini almak mümkün ise (yani x ∈ R\S olduğu hallerde) bu türev değeri sıfır olmaktadır; bu noktalar, aynen olasılık kütle fonksiyonunun sıfıra eşit olduğu noktalardır. Örneğin X rassal değişkeni bir madeni para havaya atılıp yazı-tura gelmesinin gözlemlemesi şeklinde bir deneme olsun, Bu denemenin iki mümkün sonucu vardır: yazı gelirse 0 ve tura gelirse 1. Durum uzayı olan (0,1)de X=x olasılığı 0,5 olur. Bu nedenle olasılık kütle fonksiyonu :

f_X(x) = \begin\frac, &x \in \,\\0, &x \in \mathbb\backslash\.\end

olarak ifade edilir. İçsel kaynaklar * Ayrık olasılık dağılımları

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.

Ayrık olasılık dağılımları

3 yıl önce

Olasılık kuramı içinde bir olasılık dağılımı eğer bir olasılık kütle fonksiyonu ile karakterize edilmiş ise ayrık olarak anılır. Böylelikle bir rassal...

Olasılık yoğunluk fonksiyonu

3 yıl önce

Olasılık kuramı ve istatistik bilim dallarında bir rassal değişken X için olasılık yoğunluk fonksiyonu bir reel sayılı sürekli fonksiyonu olup f ile ifade...

Birikimli dağılım fonksiyonu

3 yıl önce

kullanış kuralına göre, birikimli dağılım fonksiyonu F için, olasılık yoğunluk fonksiyonu veya olasılık kütle fonksiyonu için f kullanılmalıdır. Bu notasyon...

Olasılık teorisi

3 yıl önce

değerine eşleyen fonksiyona, yani f ( x ) {\displaystyle f(x)\,} fonksiyonuna, olasılık kütle fonksiyonu adı verilir. Modern tanım olasılık kütle fonksiyonunun...

Bozulmuş dağılım

6 yıl önce

mutlaka sabit oluşu hiç önemli değildir. Çünkü olasılık kütle fonksiyonu f(x) ve yığmalı dağılım fonksiyonu F(x), X değerinin sabit oluşuna veya nerede ise...

Negatif binom dağılımı

3 yıl önce

formel notasyon ile negatif binom için olasılık kütle fonksiyonu şöyle olur: Bu nedenle negatif binom fonksiyonu aynı zamanda gamma-Poisson bileşiği dağılım...

Negatif binom dağılımı, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu, F-dağılımı

Rademacher dağılımı

6 yıl önce

değerlerinin %50er şansla dağılmasını gösterir. Bu dağılım için olasılık kütle fonksiyonu şöyle verilir: f ( k ) = { 1 / 2 eger k = − 1 , 1 / 2 eger k...

Rademacher dağılımı, Olasılık Dağılımları, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu

Olasılık üreten fonksiyon

3 yıl önce

rassal değişken'in Olasılık üreten fonksiyonu bir rassal degiskenin olasılık kutle fonksiyonunun ureten fonksiyonu yani bir guc fonksiyonu ile temsil edilmesidir...

Olasılık Kütle Fonksiyonu