Yöney
Kısaca: Yöney veya vektör, sayısal büyüklüğü ve birimi yanında doğrultu ve yönü de olan cebirsel yapılardır. Hız, kuvvet, ivme, ağırlık ve benzerleri birer yöneysel büyüklüktür. Yöneyler bir sayı ile çarpılabilir ve bölünebilir. Yöneyler yönü değiştirilmemek şartı ile ötelenebilir. ...devamı ☟
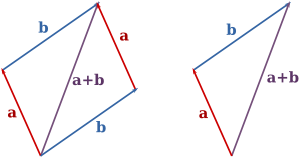
Vektör
3 yıl önceVektör veya yöney, sayısal büyüklüğü ve birimi yanında, skaler niceliklerden farklı olarak yönü de olan niceliktir. Hız, kuvvet, ivme ve ağırlık örnek...
Yöney, Ağırlık, Bağıntı, Birim öğe, Birleşme, Cebir, Dizey, Fiil, Fransızca, Hız, KoordinatVektör alanı
3 yıl önceYöney alan (vektör alanı), Öklid uzayının seçilen bir alt kümesinin her bir noktasında yöneyin belirlenmesidir. Düzlemdeki bir yöney alanı, her biri düzlemdeki...
Orhan Yöney
7 yıl önceOrhan Yöney (1942, Bursa) Türk asker. 1960 yılında Bursa Işıklar Askerî Lisesinden, 1962 yılında Kara Harp Okulu'ndan, 1963 yılında Topçu Okulu'ndan mezun...
Fazıl Osman Yöney
7 yıl önceFazıl Osman Yöney (d. 1925, Çorum), Türk siyasetçidir. Ankara Üniversitesi Siyasal Bilgiler Fakültesi mezunudur. İspir, Elmalı, Eşme, Divriği, Çarşamba...
Vektör uzayı
7 yıl önceYöney uzayı veya Vektör uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesneler (vektörler) uzayı. Daha resmi bir tanımla, bir yöney (vektör) uzayı...
Vektör uzayı, Aksiyom, Küme, Matematik, Taslak, Kartezyen çarpımını, Abelyen grupVektör hesabı
3 yıl önceVektör hesabı (vektör analizi, yöney hesabı veya yöney analizi de denilir), iki veya daha çok boyutlu (bazı sonuçlar — çapraz çarpımı içeren sonuçlar...
çapraz çarpım
3 yıl önceveya yöney çarpımı üç boyutlu uzayda iki yöney (vektör) ile yapılan bir işlemdir. Bu çarpımın sonucunda başka bir yöney elde edilir ve bu yöney çapraz...
Yöney, Ağırlık, Bağıntı, Birim öğe, Birleşme, Cebir, Dizey, Fiil, Fransızca, Gövde, HızLie cebiri
3 yıl öncebir kullanım alanı bulur. Bir cismin üzerine bu dönüşüm ile tanımlanan yöney (vektör) uzayı Lie cebri olarak adlandırılır. Adını Sophus Lie'den almıştır...