=Tanım=
- Dizey, çeşitli şekillerde tanımlanabilir. Örneğin en basit şekliyle bir dizey, sayı tablosudur. Ancak daha tutarlı ve soyut (genel) bir tanım yapılması gerekirse, dizeyi bir sayı dizisi kümesi olarak düşünebiliriz.
- Daha açık olarak dizeyleri, bileşenleri yöney (vektör) olan bir yöney (vektör) olarak düşünebiliriz.
`ler, ``m`` boyutlu yöneyler olmak üzere yöneyi bir dizey olarak tanımlanabilir.
- Tensörlerle ilişkili olacak genellikte tanımlamak istersek, bir dizey biri sütun biri kolon yöney olmak üzere iki yöneyin doğrudan çarpımıdır.
, ``n`` boyutlu bir yandeğişken (kovaryant) yöney ve de ``m`` boyutlu bir karşıdeğişken (kontravaryant) yöney olmak üzere bir dizeyin her bir bileşeni olarak tanımlanır. Burada Einstein toplam uzlaşımı kullanılmıştır. Dizeyin tam ``n.m`` tane bileşeni olduğu görülür. Eğer sadece dizeylerden bahsediyorsak, yerine gösterimi yeğlenir.
=Cebirsel İşlemler= Matematikte çarpma ile çarpım farklı kavramlardır. Çarpma bir ikili işlemdir üstelik kapalıır. Çarpım ise bir daha genel olarak bir göndermedir. Aynı şekilde toplama ile toplam karıştırılmamalıdır.
Dizey Toplaması
main|Dizey Toplaması Dizeyler bileşenleri karşılıklı olarak toplanırlar.\begin
1 & 3 & 2 \ 1 & 0 & 0 \ 1 & 2 & 2
\end+
\begin
0 & 0 & 5 \ 7 & 5 & 0 \ 2 & 1 & 1
\end=
\begin
1+0 & 3+0 & 2+5 \ 1+7 & 0+5 & 0+0 \ 1+2 & 2+1 & 2+1
\end=
\begin
1 & 3 & 7 \ 8 & 5 & 0 \ 3 & 3 & 3
\end
Sayılla (Skalerle) Çarpma
Bir dizey, bir sayıyla çarpılırsa her bileşeni o sayıyla çarpılır.\begin
1 & 8 & -3 \ 4 & -2 & 5
\end=
\begin
2\times 1 & 2\times 8 & 2\times -3 \ 2\times 4 & 2\times -2 & 2\times 5
\end=
\begin
2 & 16 & -6 \ 8 & -4 & 10
\end
Dizey Çarpımı
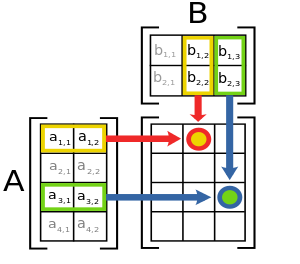
main|Dizey Çarpımı Dizey çarpımının algoritması ilk öğenin i. satırı, ikinci öğenin j. sütunuyla bileşenleri karşılıklı olarak çarpılıp toplanır ve sonuç dizeyin bileşeni olarak yazılır.``A``, ``mxn`` boyutlu ``B`` de ``nxs`` boyutlu dizeyler olmak üzere ``mxs`` boyutlu sonuç dizey
olarak tanımlanır ve her öğesi
ile bulunur.
Örnek
\begin
1 & 0 & 2 \ -1 & 3 & 1 \ \end
\begin
3 & 1 \ 2 & 1 \ 1 & 0
\end=
\begin
(1 \times 3 + 0 \times 2 + 2 \times 1) & (1 \times 1 + 0 \times 1 + 2 \times 0) \ (-1 \times 3 + 3 \times 2 + 1 \times 1) & (-1 \times 1 + 3 \times 1 + 1 \times 0) \ \end=
\begin
5 & 1 \ 4 & 2 \ \end
Çarpmayı, ilk öğenin her satırını bir yöney ve ikinci öğenin her sütununu bir yöney olarak düşünüp ilk öğeyi bir sütun yöney ve ikinci öğeyi bir satır yöney olarak yöney iç çarpımına indirgeyebiliriz. Örneğin, ve yöneyleri n boyutlu olmak üzere,
ve
şeklinde düşünüldüğünde çarpım,
biçimini alır. Bu şekilde düşünmek kağıt üzerinde dizeyleri çarparken işe yarayabilir ve zaman kazandırır.
Örnek
{|class("wikitable")
|
|
|-
|
|
|}
Kronecker (Doğrudan) Toplam
main|Doğrudan Toplam Bu toplamın sonucu bir dizeyler köşegenidir.burada sonuç dizeyin boyutları, toplanan dizeylerin doğrudan boyutları toplamı kadardır.
Kronecker (Doğrudan) Çarpım
main|Doğrudan Çarpım Bu çarpım ilk öğenin her bileşenini ikinci öğeyle doğrudan çarpmayla tanımlanır.buradan,
matematik-taslak