Türkçe Bilgi logo TürkçeBilgi

Euler Özdeşliği

Kısaca: Euler özdeşliği olarak adlandırılan ve Leonhard Euler tarafından bulunan eşitlik ...devamı ☟

Euler özdeşliği
Euler özdeşliği

Euler özdeşliği olarak adlandırılan ve Leonhard Euler tarafından bulunan eşitlik :e^ + 1 = 0, \,\! dır. Burada, :e\,\!, doğal logaritma tabanı Euler sayısını, :i\,\!, karesi -1'e eşit olan karmaşık sayıyı, :\pi\,\!, bir çemberin çevre uzunluğunun çapına oranına eşit olan pi sayısını ifade eder. Euler özdeşliği zaman zaman Euler denklemi olarak da adlandırılmaktadır. Özdeşliğin doğası Euler özdeşliği birçok matematikçi tarafından göze hoş gelen bir denklem olarak tanımlanmaktadır. Denklem, aritmetik işlemlerden toplama, çarpma ve üs almayı içerir. Euler özdeşliği matematiğin beş temel sabitini de içerir: * 0 sayısı * 1 sayısı * Trigonometri, Öklit geometrisi ve matematiksel çözümlemenin vazgeçilmez unsurlarından pi sayısı * Doğal logaritma tabanı olarak da adlandırılan e sayısı (e ≈ 2.71828) * Karmaşık sayıların temel birimi olan ve integral gibi birçok işleme izin veren i sayısı Özdeşliğe ilişkin düşünceler Mathematical Intelligencer okurları tarafından yanıtlanan bir anket sonucuna göre Euler özdeşliği matematiğin en hoş kuramıdır. Physics World tarafından 2004 yılında yapılan bir diğer anket sonucuna göre ise Euler eşitliği Maxwell denklemleri ile birlikte "gelmiş geçmiş en büyük denklemler" olarak belirlenmiştir. Paul Nahin'in Dr. Euler'in Enfes Formülü (2006) adlı kitabı Euler özdeşliğine adanmıştır. Dörtyüz sayfa uzunluğundaki bu kitap Euler özdeşliğinin "matematiksel güzelliğin zirvesine ulaştığı" kanısındadır. Constance Reid, Euler özdeşliğinin "matematiğin en önemli formülü" olduğunu öne sürmüştür. Gauss'un bu formülü ilk duyduğunda anlayamayan hiçbir öğrencinin birinci sınıf bir matematikçi olamayacağını söylediğine inanılmaktadır. 19. yüzyılın ünlü matematikçilerinden Benjamin Peirce bir dersinde özdeşliği kanıtladıktan sonra şunları söylemiştir: "Bu özdeşlik ilk bakışta çelişkili gibi duruyor ancak bunu kanıtladıktan sonra gerçeğin ta kendisiyle karşı karşıya olduğumuzu görüyoruz." Stanfordlu matematik profesörü Keith Devlin, Euler özdeşliği hakkında şunları söylemiştir: "Euler özdeşliği aşkın gerçek anlamını kavrayan bir Shakespeare sonatı ya da insanın ruhuna işleyen bir resim gibi varoluşun en derinlerine iniyor." Çıkarımı Özdeşlik, karmaşık çözümlemedeki Euler formülünün özel bir durumudur. Euler formülü her x gerçel sayısı için aşağıdaki eşitliği sağlamaktadır. : e^ = \cos x + i \sin x \,\! : x = \pi,\,\! eşitliği sağlanıyorsa : e^ = \cos \pi + i \sin \pi.\,\! ifadesi elde edilir. Bunun nedeni :\cos \pi = -1 \, \! ve :\sin \pi = 0,\,\! eşitliklerinin sağlanmasıdır. Bunun ardından aşağıdaki eşitlik elde edilir. : e^ = -1,\,\! ve bu eşitlik bizi Euler özdeşliğine götürür. : e^ +1 = 0.\,\! Euler Bağıntıları : e^ = cos(x)+isin(x)\! : e^ = cos(x)-isin(x)\! : cos(x) = (e^+e^)/2\! : sin(x) =(e^-e^)/2\,i\! double euler(double exp.'e atfen) bağıntıları : e^} = e^\! : e^} = e^\,\! : e^} = e^\,\! : e^\,=(}+e^}})/ \! : e^\,=(}-e^}})/\,i \! Genelleme Euler özdeşliği aşağıda formülü verilen eşitliğin n= 2 durumunu sağlar. :\sum_^ e^ = 0 . Atıf sorunu Euler, formülünün e sayısını cos ve sin terimleriyle ilişkilendirdiğini birçok yerde belirtmiştir ancak Euler'in kendi adına atfedilen özdeşliği bulduğuna dair somut bir kanıt bulunmamaktadır. Bazı kaynaklar bu özdeşliğin Euler'in doğumundan önce kullanılmakta olduğunu öne sürmektedirler. (Durum böyleyse bu, Stigler adlandırma yasasına bir örnek oluşturabilir.) Bu nedenle, özdeşliğin Euler'e atfedilmesinin uygun olup olmadığı konusunda genel bir kabul yoktur. Ayrıca bakınız * Üstel fonksiyon * Gelfond sabiti Notlar * Crease, Robert P., " Gelmiş geçmiş en büyük denklemler", PhysicsWeb, Ekim 2004. * Crease, Robert P. " Simgesel Denklemler," PhysicsWeb, Mart 2007. * Derbyshire, J. Büyük Takıntı: Bernhard Riemann ve matematiğin en gizemli sorusu (New York: Penguin, 2004). * Kasner, E. ve Newman, J., Matematik ve Hayalgücü (Bell ve Sons, 1949). * Maor, Eli, e: Bir Sayının Öyküsü (Princeton University Press, 1998), ISBN 0-691-05854-7 * Nahin, Paul J., Dr. Euler'in Enfes Formülü (Princeton University Press, 2006), ISBN 978-0-691-11822-2 * Reid, Constance, Sıfırdan Sonsuza (Amerikan Matematik Kurumu). * Sandifer, Ed, " Euler'in En Büyük Başarıları", MAA Online, Şubat 2007.

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Euler özdeşliği Resimleri

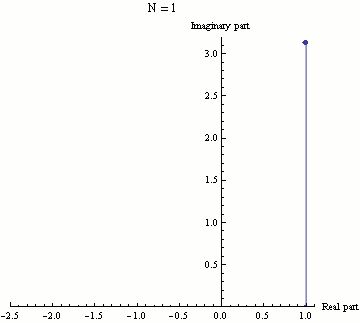
Euler Formülü
6 yıl önce

{\displaystyle x=\pi } eşitliği sağlandığında Euler formülü: eiπ + 1 = 0 halini alır ve buna Euler özdeşliği denir. Bu formül ei φ {\displaystyle \varphi...
Euler (anlam ayrımı)
6 yıl önce

Euler şu anlamlara gelebilir: Leonhard Euler - İsviçreli matematikçi ve fizikçi. Euler formülü - Euler'in bulduğu, karmaşık üstel fonksiyonlarının sin...
Leonhard Euler
3 yıl önce

sin, cos ve tan tanımlamalarıdır). Euler'in babası Paul Euler ve annesi Marguerite Brucker'dı. Babası Paul Euler Protestan papazıydı ve oğlunun da kendi...

Leonhard Euler, 15 Nisan, 1707, 1726, 1727, 1730, 1733, 1734, 1735, 1740, 1741
Logaritma
3 yıl önce

Leonhard Euler dir. Euler özdeşliği yardımıya negatif sayıların logaritması alınabilir. Bu logaritmayı alabilmek için logaritmanın özellikleri ve Euler özdeşliği...

Logaritma, Gelenbevi İsmail Efendi, John Napier, Reel sayı, Joost Bürgi, Uygulamalı matematik
Jean Gaston Darboux
3 yıl önce

Darboux formülü Christoffel–Darboux özdeşliği Christoffel–Darboux formülü Euler–Darboux denklemi Darboux–Froda teoremi Euler–Poisson–Darboux deklemi 1870. Sur...
Hiperbolik fonksiyon
3 yıl önce

{1}{x}}} Hiperbolik sinüs ve kosinüs, Pisagor trigonometrik özdeşliği'ne benzeyen aşağıdaki özdeşliği sağlar cosh 2 ⁡ x − sinh 2 ⁡ x = 1 {\displaystyle \cosh...
Zeta sabiti
3 yıl önce

} Pozitif çift tam sayılar kümesi Euler tarafından bulunan ve Bernoulli sayılarıyla ilintilendirilen şu özdeşliği içerir: ζ ( 2 n ) = ( − 1 ) n + 1 B...
Trigonometrik fonksiyonlar
3 yıl önce

}{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}} Bu iki serinin şu toplamı Euler formülü'nü verir: cos x + i sin x = eix. Diğer serilerde bulunabilir. Aşağıdaki...

Trigonometrik işlevler, Açı, Dik üçgen, Geometri, Matematik, Pisagor teoremi, Seri (matematik), Taslak, Üçgen, İşlev, Trigonometrik ifadeler listesi