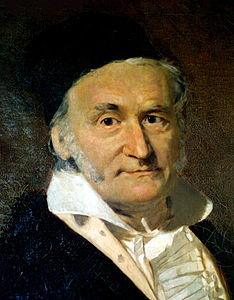Gauss'un çocukluk yıllarından beri dahi olduğunu gösteren pek çok hikaye vardır, nitekim pek çok matematiksel keşfini henüz 20 yaşına gelmeden yapmıştır. Sayılar kuramının önemli sonuçlarını derleyip kendi katkılarını da ekleyerek yazdığı büyük eseri Disquisitiones Arithmeticae'yi 21 yaşında (1798) bitirmişse de, eser ilk olarak 1801'de basılmıştır.
Hayatı
Çoçukluğu ve gençliği
Gauss, Kutsal Roma Cermen İmparatorluğu'na bağlı olan Braunschweig-Lüneburg Dükalığı'ndaki Braunschweig kentinde, Gebhard Dietrich ve Dorothea Gauss çiftinin tek çocuğu olarak dünyaya geldi. Babası az eğitimli bir taş ve duvar ustasıydı, annesinin ise okuma-yazması bile yoktu. Efsaneye göre, Gauss henüz üç yaşındayken, babasının kağıt üzerinde yaptığı hesapları kafasından kontrol edip düzelterek dehasını belli etti.Bir başka meşhur hikayeye göre, Gauss'un ilkokul öğretmeni J.G. Büttner, öğrencilerini oyalamak için 1'den 100'e kadar olan sayıları toplamalarını isteyince, Gauss cevabı birkaç saniye içinde bularak hem öğretmenini, hem de asistanı Martin Bertels'i hayrete düşürdü. Küçük Gauss, sayı listesinin iki zıt ucundan birer sayı alıp topladığında hep aynı sonucun çıktığını farketmişti: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, vesaire. Böylece 1'den 100'e kadar olan sayıların toplamı 50 × 101 = 5050 oluyordu.
Gauss, Braunschweig Dükü Karl Wilhelm Ferdinand'in verdiği burs sayesinde 1792-1795 arasında Collegium Carolinum'da (bugünkü adıyla Braunschweig Teknik Üniversitesi), 1795-1798 arasında da Göttingen Üniversitesi'nde öğrenim gördü. 1796'da kenar sayısı bir Fermat asalı olan her düzgün çokgenin, sadece cetvel ve pergel kullanılarak çizilebileceğini kanıtladı. Bu tür cetvel ve pergel problemleri Antik Yunan'dan beri matematikçileri meşgul etmekteydi, dolayısıyla da Gauss'un keşfinin önemi büyüktü. Gauss bu başarısından o kadar memnun oldu ki, mezar taşına bir düzgün onyedigenin oyulmasını vasiyet etti. Ne var ki, daireye çok yakın olan bu şeklin oyulması çok zor olacağından, vasiyetini yerine getirecek bir taş ustası bulamadı.
1796 Gauss için oldukça verimli bir yıl oldu. Düzgün çokgenlerle ilgili keşfinden bir ay kadar sonra, yine kendi keşfi olan modüler aritmetik fikrini kullanarak, sayılar kuramında "karesel karşılıklılık ilkesi" (Alm. quadratisches Reziprozitätsgesetz) olarak bilinen çok önemli teoremi kanıtladı. İlk olarak Euler ve Legendre tarafından ortaya atılmış ama kanıtlanamamış olan bu teorem, ikinci dereceden denklemlerin çözülebilirliğinin belirlenmesini sağlıyordu. Yine aynı yıl içinde Gauss, asal sayıların tamsayılar arasındaki dağılımına ilişkin önemli bir sonuç buldu. Bundan kısa bir süre sonra da, her tamsayının en fazla üç üçgensel sayının toplamı olarak yazılabileceğini kanıtladı, ve 10 Temmuz 1796'da günlüğüne şu notu düştü: "Eureka! Num = Δ + Δ + Δ." Ekim 1796'da ise katsayıları sonlu bir cisimden gelenpolinomların çözümleriyle ilgili bir sonuç yayımladı. (Bu sonuç, 150 yıl sonraki Weil varsayımlarının da çıkış noktası olmuştur.)
Orta yaşları
Gauss, 1799'da bitirdiği doktora tezinde cebirin temel teoreminin bir kanıtını sundu. Bu çok önemli teorem, karmaşık sayılar üzerine tanımlanmış her polinomun en az bir kökü olduğunu söyler. Gauss'tan önce pek çok matematikçi bu teoremi kanıtlamayı denemiş, ama hiçbir kanıt genel kabul görmemişti. Gauss'un kanıtına da, o zamanlar henüz kanıtlanmamış olan Jordan eğri teoremini kullandığı için itiraz edildi. Bu itirazlar üzerine Gauss, hayatı boyunca üç değişik kanıt daha sunacak, 1849'daki son kanıtı tüm matematikçilerden kabul görecekti. Gauss bu kanıtlar üzerinde çalışırken, karmaşık sayılar kavramının olgunlaşmasına çok büyük katkıda bulundu.1801'de yayımladığı Disquisitiones Arithmeticae, sayılar kuramına modüler aritmetik gibi bir çok yenilik getirdi. Aynı yıl içinde, İtalyan astronom Giuseppe Piazzi, Ceres asteroidini keşfetti, ama asteroidi ancak 40 gün kadar takip edebildikten sonra kaybetti. 24 yaşındaki Gauss, üç aylık bir çalışmadan sonra, Ceres'in tekrar görülebileceği pozisyonu hesapladı, ve 31 Aralık'ta iki ayrı astronom (Franz Xaver von Zach ve Heinrich Olbers), Ceres'i tam Gauss'un söylediği pozisyonda gözlemlediler. Zach, "Doktor Gauss'un zeki çalışması ve hesapları olmasaydı, Ceres'i tekrar bulamayabilirdik" diyerek Gauss'un katkısına teşekkür etti. O zamana kadar hala Dük'ün verdiği bursla geçinen ve bu durumdan memnun olmayan Gauss, astronomide kariyer yapmayı düşündü, ve 1807'de Göttingen Üniversitesi'nde astronomi profesörü ve gözlemevi müdürü olarak çalışmaya başladı. Hayatının sonuna kadar aynı üniversitede çalışacaktı.
Ceres'in keşfi sayesinde gezegen ve asteroidlerin Güneş çevresindeki hareketleriyle ilgilenmeye başlayan Gauss, 1809'da "Theoria motus corporum coelestium in sectionibus conicis solem ambientum" (Güneş çevresinde konik kesitler üzerinde hareket eden gök cisimlerinin hareketlerinin teorisi) adlı eserini yayımladı. Bu eser, günümüz bilimlerinde yaygın olarak kullanılan en küçük kareler yöntemini de ayrıntılı olarak ele alıyordu. (Aynı yöntem, 1805'te Fransız matematikçi Adrien Marie Legendre ve 1808'de Amerikalı matematikçi Robert Adrain tarafından da tanımlanmış ve kullanılmıştı, fakat Gauss bu yöntemi 1795'den beri bildiğini iddia etti.
Gauss en karmaşık hesapları aklından yapabilmesiyle de ünlenmişti. Anlatılana göre, Ceres'in izleyeceği yörüngeyi nasıl bu kadar hatasız hesaplayabildiği sorulunca, "logaritma kullandım" cevabını vermiş, logaritma cetvelini nasıl bu kadar hızlı kullanabildiği sorulunca da "cetvele ne gerek var, hepsini kafamda hesaplıyorum!" demiştir.
1818'de Hannover eyaleti için yüzey ölçümleri yapan Gauss, bu ölçümler için helyotropu (güneş ışığı ve aynalar yardımıyla mesafe ölçmeye yarayan bir aygıt) icat edip kullandı.

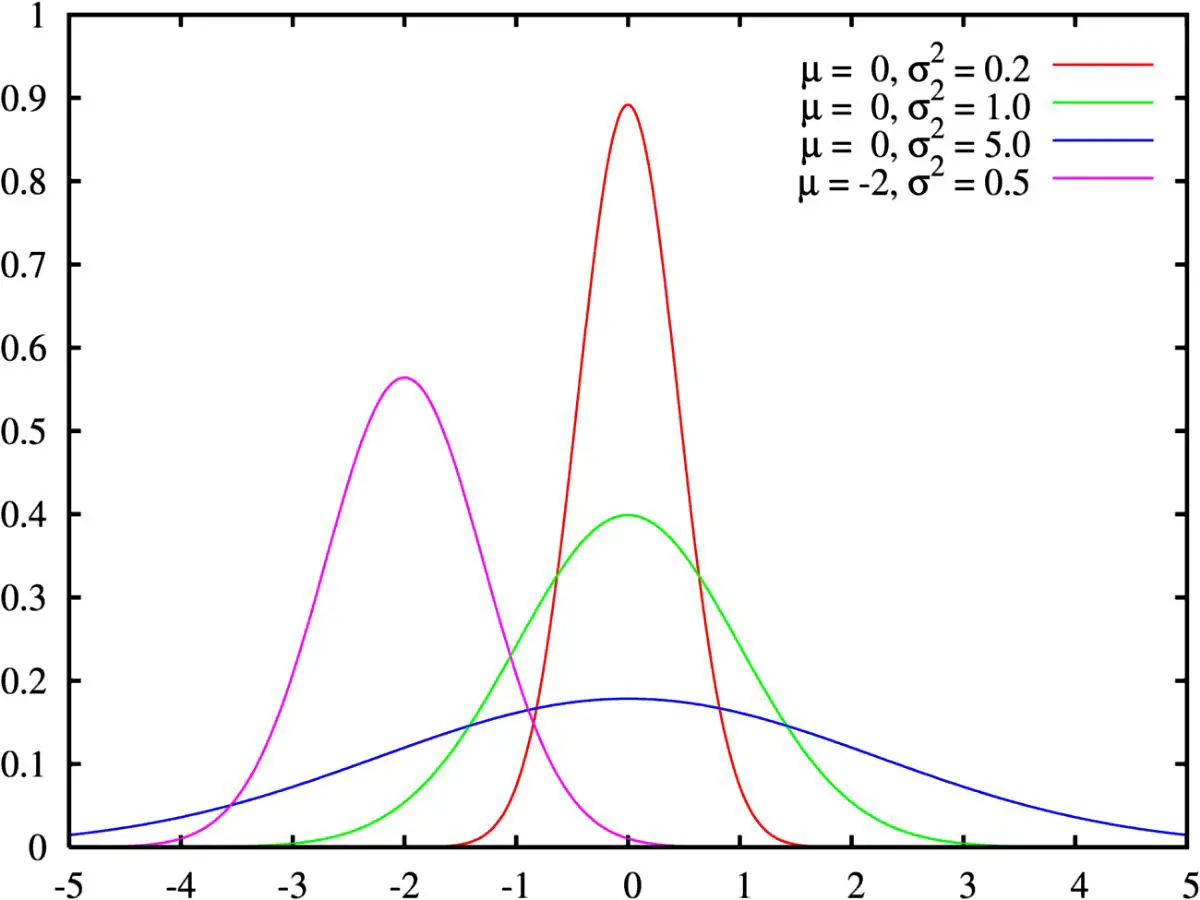
Gauss, Hannover'de yaptığı yüzey ölçümleri sırasında, ölçüm hatalarının istatistiksel dağılımını veren (ve daha önce astronomi araştırmalarında da kullandığı) normal dağılım fikrini kafasında iyice belirginleştirdi. (Bugün normal dağılıma Gauss dağılımı da denmektedir.) Ayrıca bu ölçümler Gauss'un diferansiyel geometriye de (eğriler ve yüzeylerle ilgilenen bir matematik dalı) ilgi duymasını sağladı. 1828'de bu matematik dalının önemli teoremlerinden biri olan theorema egregium'u kanıtladı.
Yaşlılığı ve ölümü
1831 yılında Gauss, fizik profesörü Wilhelm Weber'le beraber çalışmaya başladı. Bu beraberlik, manyetizma ve elektrik konularına pek çok yenilik getirecekti (kütle, uzunluk ve zamana bağlı yeni bir manyetizma birimi gibi). 1833'te Gauss ve Weber ilk elektromanyetik telgrafı icat ettiler, ve bu telgrafla gözlemevini fizik enstitüsüne bağladılar. Gauss, hala müdürü olduğu gözlemevinin bahçesine bir manyetik gözlemevi kurulması talimatını verdi, ve Weber'le beraber Dünya'nın çeşitli yerlerindeki manyetik alanı ölçmek amacıyla bir "manyetik kulüp" (Alm. magnetischer Verein) kurdu. Gauss'un bu sıralarda geliştirdiği, manyetik alanın yatay yoğunluğunu ölçmeye yarayan metod, 20. yüzyıl ortalarına kadar kullanılmaya devam etti. Gauss ayrıca, Dünya'nin manyetik alanının iç (çekirdek) ve dış (manyetosfer) kaynaklarını ayırmak için gereken matematiksel teoriyi de geliştirdi. Hayatının sonlarına doğru matematiksel yeteneklerinin köreldiğini hissedince edebiyatla ilgilenmeye başladı.Gauss 23 Şubat 1855'te, 78 yaşındayken, yıllardır yaşadığı Göttingen'de hayata gözlerini yumdu ve bu şehirdeki Albanifriedhof 'a gömüldü. Cenazesinde damadı Heinrich Ewald ve yakın arkadaşı (aynı zamanda biyografisinin yazarı) Wolfgang Sartorius von Waltershausen birer konuşma yaptılar. Beyni araştırma için muhafaza edildi, ve bugün hala Göttingen Üniversitesi'nin tıp fakültesinde formalin içinde korunmaktadır.
Aile hayatı
Gauss ilk evliliğini 1805 yılında Johanna Osthoff ile yaptı. Bu evlilikten Joseph (1806-1873) adında bir oğlu ve Wilhelmine (1808-1846) adında bir kızı oldu. 1809'da, Louis adını verdikleri üçüncü çocuğun doğumu sırasında Johanna hayatını kaybetti, Louis de henüz bir yaşına gelmeden annesini takip etti. Gauss, bu ölümlerden dolayı girdiği depresyondan asla tam anlamıyla kurtulamadı. Louis'in ölümünden kısa süre sonra, 1810'da karısının arkadaşı Minna Waldeck ile evlendi. Bu evlilikten de üç çocuğu oldu: Eugen (1811-1896), Wilhelm (1813-1879) ve Therese (1816-1864). Minna 1831'de hastalıktan ölünce Gauss'a ölümüne kadar kızı Therese baktı. Eugen ve Wilhelm ABD'nin Missouri eyaletine yerleştiler.Kişiliği
Gauss tam bir mükemmeliyetçi ve bir işkolikti. Bir hikayeye göre, bir problem üzerinde çalışırken karısının ölmek üzere olduğu haberini alınca "biraz beklesin, bitirmek üzereyim" demişti.Kafasındaki fikirler tam olgunluğa erişmeden onları yayımlamak istemezdi. Bu konudaki ilkesini pauca sed matura (az ama olgun) sözüyle özetliyordu. Ölümünden sonra incelenen günlükleri ortaya çıkardı ki, meslekdaşları tarafından yayımlanmış olan pek çok önemli matematiksel keşfi o daha önceden yapmış, ama yayımlamamayı tercih etmişti. Matematik tarihçisi Eric Temple Bell'e göre, Gauss günlüklerine yazdığı tüm matematiksel fikirleri hayattayken yayımlamış olsaydı matematik 50 yıl ileri atlamış olurdu.
Gauss, kendisini örnek alan genç matematikçileri desteklemediği için çok eleştirildi. Pek çok meslekdaşı onu mesafeli ve katı buluyordu. Gauss öğretmenlikten nefret ettiğini söylese de Richard Dedekind, Bernhard Riemann, Friedrich Bessel gibi bazı öğrencileri sonradan başarılı ve üretken matematikçiler oldular.
Gauss'un babasıyla arası iyi değildi. Babası Gauss'un matematik ve bilim okumasını istemiyor, kendisi gibi taş ustası olmasını istiyordu. Gauss, eğitimi boyunca babasından görmediği desteği annesinden gördü. Oğullarıyla da iyi geçinemeyen Gauss, Eugen'in ve daha sonra Wilhelm'in ABD'ye göç etmesine sebep oldu.
Gauss, yazdığı zeki kanıtları nasıl akıl ettiğini asla açıklamazdı. Kanıtı bir kere bulduktan sonra sanki vahiyle gelmiş gibi yazar, sonuca nasıl ulaştığı konusunda özellikle ipucu vermezdi.
Oldukça dindar ve muhafazakar bir adamdı. Ayrıca bir monarşi destekçisiydi ve tüm Almanya'yı etkisi altına alan 1848 devrimlerini onaylamıyordu.
Anma
Gauss'un ismi matematik ve fizikte onlarca teorem, formül ve kavrama verilmiştir. Cgs sistemindeki manyetik alan birimi 1 Gauss'tur.1989-2001 yılları arasında Gauss'un resmi, bir normal dağılım eğrisiyle beraber, 10 DM banknotlarının üzerine basılmıştır.
1977'de, Gauss'un 200. doğumgünü şerefine, Doğu Almanya ve Batı Almanya'da ayrı ayrı hatıra pulları basılmıştır.
Ay'daki Gauss krateri, "1001 Gaussia" asteroidi ve Antarktika'da sönmüş bir volkan olan Gaussberg, Gauss'un anısına isimlendirilmiş bazı doğal oluşumlardır.
Almanya'nın Dransfeld kentindeki 51 metrelik beton gözlem kulesinin ismi Gauss Kulesi'dir.
Alman yazar Daniel Kehlmann'ın 2005 tarihli romanı Die Vermessung der Welt (Dünya'nın Ölçümü), Gauss ve Alexander von Humboldt'un hayatlarını konu almaktadır.
Matematik ve Gauss (Çalışmaları)
Daha çocuk yaşlarda rakamları parmağında oynatmaya başlayan Gauss, "Matematiğin Prensi" olarak anılıyor. Matematikten astronomiye, fiziğe kadar pek çok dalda yeni keşiflere imza atan dahi, günümüzde gerçekleştirilen bilimsel araştırmalara da ışık tutuyor.Ressam Christian Albrecht Jensen, 1850'de Gauss'un portresini yapmıştı. Geçtiğimiz nisan ayında, dünya basınında yayımlanan bilimsel bir keşfin haberi sevinçle karşılandı. Astronomların oluşturduğu uluslararası bir ekip, günümüzden 15 milyar yıl önce meydana gelen ve evreni doğuran "Büyük Patlama"dan geriye kalan sıcaklığı incelemişti. Bu "sıcak lekeler"in çözümlenmesi sırasında, ekip, şaşkınlık uyandıran bir sonuca ulaşmıştı: "Evreni oluşturan uzayın yapısı düzdür."
Pek çok kişi, uzayın bir şekle sahip olması fikrinin imkansızlığına inanıyor. Bunun yanı sıra, bilim adamlarına göre, tartışma yaratan son iddianın geçmişi 150 yılı aşkın bir süreye uzanıyordu. Tüm zamanların en büyük matematikçisi Carl Friedrich Gauss'a. Bu kozmik keşif, Gauss'un fikirlerinin hala geçerli olduğunun bir göstergesi. Herhangi bir bilim sözlüğü karıştırıldığında, istatistikten savaş konularına pek çok alanda ürettiği teoriler bulunabilir. İstatistik alanında, nüfus eğilimlerini açıklamakta hayati önem taşıyan çan şeklindeki "Gauss eğrisi" ya da bir nükleer denizaltının manyetik alanını nötrleştirmesi şeklinde tanımlanan "degauss"lama, bunlardan sadece ikisi.
Gauss, diğer matematikçilerden farklı olarak, salt matematikten ilgi alanına giren konulara yönelik çalışmalara kadar, çok farklı alanlarda kilit buluşlara imza attı. Yapıtlarıyla matematik dünyasına yeni bir soluk getirmişti. Bu nedenle de, bilim çevresinde "Matematiğin Prensi" olarak adlandırılıyor.
Daha çocukluğunda, erken gelişmiş zekası ve matematiğe karşı yeteneğiyle sivrildi. İşçi kökenli anne babanın oğlu Gauss, 1777'de Almanya'nın Brunswick kentinde doğdu. Babasının yaptığı hesapları izlediği sırada, ailesi onun ileri düzeydeki zekasını keşfetti. Küçük Carl, babasının yanlışını bulmuş ve doğru cevabı söylemişti. Hesapları tekrar kontrol eden babası hayrete düşmüştü. Çünkü, 2 yaşında oğlunun ikazı doğruydu.
10 yaşındaki Gauss'un matematiksel yeteneği, en iyi öğretmenlerini bile geride bırakıyordu. Matematik dersinin ilk gününde, Gauss ve sınıftaki diğer gözde öğrenciler, aritmetik dizin şeklinde adlandırılan konu üzerine yoğunlaştılar. Amaçları, ardışık sayılara 371, 413, 455... gibi sayıları eklemek ve bu sabit sayılar arasındaki farklılıkları anlamaktı. Gauss, bulduğu çözümü ilan etmeden önce, öğretmenleri problemin ne olduğunu büyük zorluklarla açıklamıştı.
Sınıftaki diğer arkadaşlarının, onun çabucak ulaştığı çözümü bulmaları neredeyse bir saati almıştı. Bu tür dizinleri formülleştirmeye çalı gerekli bağlantıları kurmuş ve problemi çözmüştü. Bunların hepsini de, neredeyse ışık hızıyla akıldan hesaplamıştı. Gauss'un aritmetiğe matematiğe duyduğu bu olağanüstü eğilim, Brunswick dükünün ilgisini çekti ve hemen okul masraflarını üstlendi.
Genç Gauss, kolej yıllarında, dikkatini, aralarında Newton'un da bulunduğu ünlü akademisyenlerin büyük çalışmalarına yöneltti ve ilk özgün araştırmalarını gerçekleştirdi. Gauss'un erken yaşlarda ulaştığı matematiksel zaferler, daha sonraki kariyerinin de habercisiydi. 19 yaşındayken, bütün rakamların özelliklerini bir bir açıklayınca, o güne kadar geçerli matematik yasalarını alt üst etti. Dahası, gözlemler sonucu bulunan veri noktalarından geçecek en uygun eğimin belirlenmesinde kullanılan "En Küçük Kareler Metodu"nu keşfetti. Ayrıca, asal sayılarla, üçgen, kare, beşgen gibi geometrik şekiller arasındaki bağlantıları buldu. Keşfettiği bağıntıları kullanarak da, antik Yunan geometricilerinin bile gerçekleştirmeyi başaramadığı 17 kenarlı çokgeni kurdu. Bu başarılarından sadece biri bile, Gauss'un matematikçiler dünyasındaki egemenliğini kanıtlamaya yetiyordu. Ancak bu, onun için sadece bir başlangıçtı. Göttingen Üniversitesi'ne kabul edilen dahi, 22 yaşındayken doktorasını tamamladı ve bütün cebir denklemlerinin çözümlerini sunduğu ilk kez kanıtlanan "Temel Cebir Teoremi"ni yarattı. Ama, tüm başarılarına rağmen hak ettiği ünü bir türlü kazanamamıştı. Ta ki 1801 yılına, bir İtalyan astronomun Mars ve Jüpiter arasında bir gezegen bulduğunu açıklamasına kadar... Diğer astronomlar da bu iddiayı kanıtlamak için yarıştılar. Ancak, yeni gezegen, güneşin göz kamaştıran ışınları arasında kaybolmuştu. Bilim adamları, gezegenin yerini saptamak konusunda başarılı olamıyorlardı. Gauss, adını duyurabilecek bir şans yakalamıştı.
En Küçük Kareler Metodu'nu yeni gezegenle ilgili gözlemlere uygulayarak, nerede görülebileceğini belirledi. Bundan birkaç ay sonra astronomlar, Gauss'un öngördüğü yere teleskoplarını yönlendirdiler ve gerçekten de gezegeni buldular. Astronomlar bu gezegene "Ceres" adını verdiler. Ceres, günümüzde, Mars ile Jüpiter arasındaki yörüngede bulunan binlerce kaya parçası içindeki ilk "küçük gezegen" ya da asteroit olarak biliniyor.
Gauss'un bu buluşu, uluslararası alanda tanınmasına yol açtı. Bu sırada, sadece 24 yaşındaydı. Kendisine ün kazandıran gelişmeden birkaç ay sonra, ikinci bombasını patlatacak, matematik alanında en önemli çalışmalardan biri kabul edilen Aritmetik Araştırmalar (Disquisitiones Aritmeticae) adlı kitabını yayımlayacaktı. Kitabında, asal sayılar gibi bütün sayıların özellikleriyle ilgilenen matematiğin yeni dalı "sayı teorisi"ni incelemişti.
Çalışması, günümüzde de kullanılan sayı teorisinin temelini oluşturuyor. 1807 yılında, Göttingen Üniversitesi astronomi bölümüne profesör oldu ve ömrünün sonuna kadar da burada kaldı. Dahi bilim adamı, 31 yaşında ikinci başyapıtını yayımladı. Konik Kesitli Gökcisimlerin Güneş Çevresindeki Hareket Kuramı (Theoria Motus Corporum Coelestium in Sectianibus Conicis Solem Ambientium) başlıklı yapıtında, Güneş Sistemi içindeki gezegenlerin çekim kuvvetlerinin hesaplanmasını ve yörünge kuramlarını gösterdi. Sunduğu yöntemler, bugün bile astronomlar tarafından kullanılıyor.
Gauss, 1777'de Brunswick'teki bu evde doğmuştu. Bu yapı, II. Dünya Savaşı sırasında yıkıldı. Gauss, bu çalışmasından sonra dikkatini Dünya'ya çevirdi. 4.000 yıldır Dünya'nın kusursuz bir küre olduğu düşünülmüştü. Ancak, Isaac Newton Dünya'nın yörüngesel hareketi gereği ekvator düzleminde bir bombenin var olduğunu göstermişti. Gauss, Dünya'nın şeklini nasıl ölçebileceğini araştırırken, köklü bir keşfe daha imza attı: "Herhangi bir yüzeyin şekli, geometrinin normal kuralları ona hala uygulanabiliyorsa ölçülebilir."
2.000 yıl önce Yunanlı matematikçi Eukleides, bu kuralları belirlemişti. Örneğin, paralel doğrular, uzunlukları ne olursa olsun kesişmezler gibi. Ancak Gauss, Eukleides'in paralel doğruların kesişmeyecekleri ilkesini düz yüzeyleri göz önünde bulundurarak açıkladığını fark etti. Top ya da gezegen gibi kıvrımlı yüzeylerde, Eukleides yasası geçerliliğini yitiriyordu. Zaten boylamların ekvatorda paralel olarak başlayıp, daha sonra kutuplarda kesişmesi, bunun en açık kanıtı.
Bu yaklaşımı, Eukleides-dışı geometriye doğru giden yolda ilk adımdı. Dolayısıyla, o güne kadar yürütülen tüm çalışmalar bir anlamda değerini yitiriyordu. Örneğin, Eukleides-dışı yüzeylerde, bir üçgenin iç açılarının toplamı artık 180 derece değildi ya da bir çemberi çevre çapıyla Pi sayısının çarpımına eşit değildi.
Gauss, bütün bunları içeren formülleri belirledi. Bu bağlamda, haritacıların neden dünyanın mükemmel bir haritasını çizemeyeceklerini açıkladı: "Bir kürenin yüzeyi gerçek bir eğime sahiptir, dolayısıyla bu doğal eğimleri bilmeden haritanın ayrıntıları belirlenemez. Buna karşılık, bir silindirin eğimli yüzeyi mükemmel bir şekilde düzleştirilebilir. O nedenle, dünya haritalarında çok farklı modeller deneniyor ve aslında eğimli olmasına karşın, düz yüzeylerde yansıtılıyor."
Bu kilit keşiflere rağmen Gauss, Eukleides-dışı geometriyle ilgili çalışmalarını büyük bir gizlilik içinde yürüttü. Ne de olsa 2000 yıllık bir geçmişle hesaplaşıyordu. Yıllar sonra, diğer araştırmacılar da benzer sonuçlara ulaştılar ve bunları açıklamaya başladılar. Harekete geçen bilim adamlarının arasında Albert Einstein da vardı. Einstein, 1915 yılında, yeni geliştirdiği Genel İzafiyet Teorisi'nin merkezine Eukleides-dışı geometriyi oturtmuştu.
Genel İzafiyet Teorisi'ne göre, yerçekimi, uzay ve zamanın kütlesel eğiminin bir sonucuydu. Eğrisel ve sonlu olarak düşünülen dört boyutlu bir evrene ait çekim teorisiydi. Ancak, Genel İzafiyet Teorisi'ne göre evren, hem bir bilardo masası gibi sıfır eğrilik derecesine sahip olabilir, hem de bir top gibi pozitif eğimli ya da bir semer gibi negatif eğimli olabilirdi.
Geçtiğimiz nisan ayında, astronomların uzayın derinliklerinde Büyük Patlama'dan geriye kalan sıcaklığı çözümlemeleri sırasında ortaya çıkan sonuç, Gauss'un eğimli yüzeylerin ölçülebileceği iddiasını doğruluyor. Nitekim, astronomlar, evrenin eğimini ölçtüler ve sonuçta da dün olduğu sonucuna ulaştılar.
Bir denizaltının üzerindeki manyetik alan. 1830'lu yıllarda Gauss, 50'li yaşlara merdiven dayamıştı; ancak hala yeni araştırma alanları arıyordu. Alman fizikçi Wilhelm Weber ile bir ekip kurup, o günlerde büyük bir karmaşa yaratan elektromanyetizma teorisini yeniden ele aldı. Manyetizmanın ölçülmesine yönelik çok hassas yeni birimler oluşturdu. Bunlar arasında "Gauss" birimi, günümüzde de kullanılıyor. Ayrıca, elektromanyetik yüklerin etkileri hakkında çok önemli teoremlere ulaştı. Bundan sonraki araştırmalarında, geometrik şekillerin veya üç boyutlu cisimlerin bazı durumlarda değişmeyen özelliklerini inceleyen matematik dalı olan "topoloji" üstünde yoğunlaştı. Topoloji, bükülen, eğrilen cisimleri inceliyordu. Gauss, bu dalın evreni kavramakta çok önemli bir yere sahip olduğunu düşünüyordu. Tarih, bu konuda da Gauss'u haklı çıkardı. Çünkü topoloji, bugün teorik fiziğin kalbini oluşturuyor.
Evrendeki parçacıkların özellikleri ve aralarındaki güç ilişkisi, topolojinin yardımıyla açıklanıyor. Gauss, 1855 yılında 78 yaşındayken ölmüştür. Hayatını matematiğe adayan bilim adamı, sayılarla oyun oynamayı kendisine görev bilmişti. Günümüze kadar uzanan teorileri, matematiğe ışık tutmayı sürdürüyor.
Gauss'un ünlü Çan Eğrisi
Kolej öğrencilerinin IQ'sundan zürafaların ağırlığına kadar, günlük hayata ilişkin pek çok değer, çan eğrisini izliyor ve Gauss adının önemin artırıyor. Matematiksel değerlerin incelenmesine yarayan bu eğriye de, ünlü matematikçinin adından gelen Gauss eğrisi deniliyor. Bu eğri, ilk kez Fransız matematikçi Abraham de Moivre tarafından, 1733'te keşfedilmekle birlikte, Gauss tarafından yeniden tanımlandı ve değerlendirmelerde kullanılan matematiksel işlemler, onun tarafından gerçekleştirildi. Eğri, örneğin insanların IQ düzeylerinin belirlenmesinde ortalamayı yansıtıyor. Bu da, ortalamanın altındaki ve üstündeki IQ'nun ortaya çıkmasını sağlıyor.İlkede, orta noktası doruğa ulaşan herhangi bir eğri de aynı işlevi görüyor. Ancak Gauss, gelişigüzel etmenler nedeniyle bir yayılma söz konusuysa, eğrinin belirgin bir şeklinin olması gerektiğini belirtiyor. Zaten, bunun için bir formül de geliştirmiş ve eğriye çan şeklini uygun görmüş. Bu eğri her alana uygulanamıyor. Sözgelimi radyoaktif bozulma gibi. Ancak, eğrisi, iki sayı arasında doğru çizilmeye olanak tanıyan birçok olgunun açıklanmasında işe yarıyor. Bu durumda, ortalama değer, çan eğrisinin doruk noktasını oluşturuyor. Standart sapma da eğrinin diğer tarafa geçiş eğilimini sergiliyor. Bu iki sayı arasındaki bağıntı yüzde oranını veriyor. Örneğin, bir kişinin boyunun ortalamanın ne kadar altında ya da üstünde olduğunun belirlenmesi gibi.
kaynak:vikipedi