Türkçe Bilgi logo TürkçeBilgi

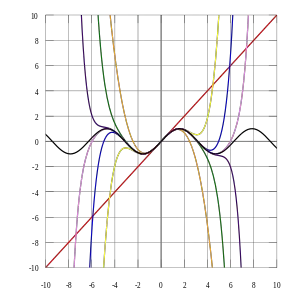
Taylor Serisi

Kısaca: Taylor serisi matematikte, bir fonksiyonun, o fonksiyonun terimlerinin tek bir noktadaki türev değerlerinden hesaplanan sonsuz toplamı şeklinde yazılması şeklindeki gösterimi/açılımıdır. Adını İngiliz matematikçi Brook Taylor'dan almıştır. ...devamı ☟

Taylor serisi
Taylor Serisi

Matematikte, her mertebeden türevli bir f(x) fonksiyonunun (a-r,a+r) aralığındaki Taylor serisi aşağıdaki şekilde tanımlanmıştır: 

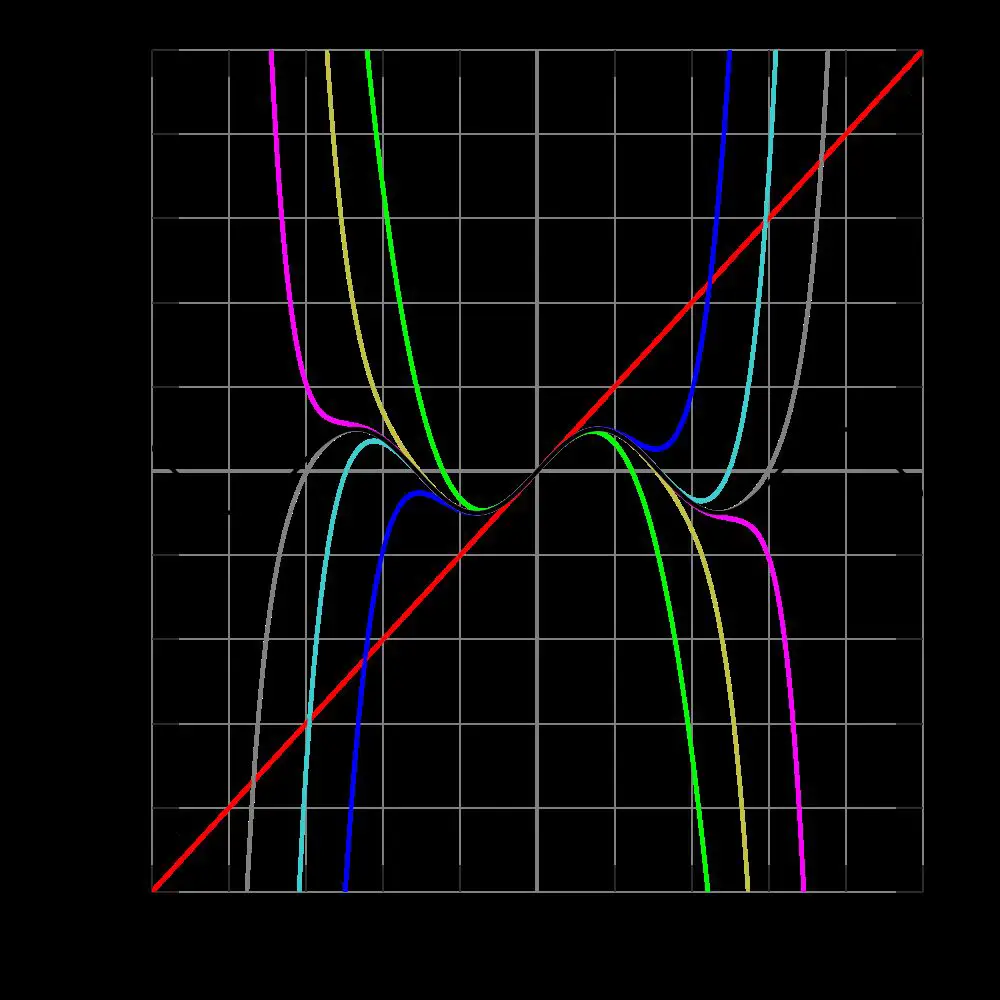
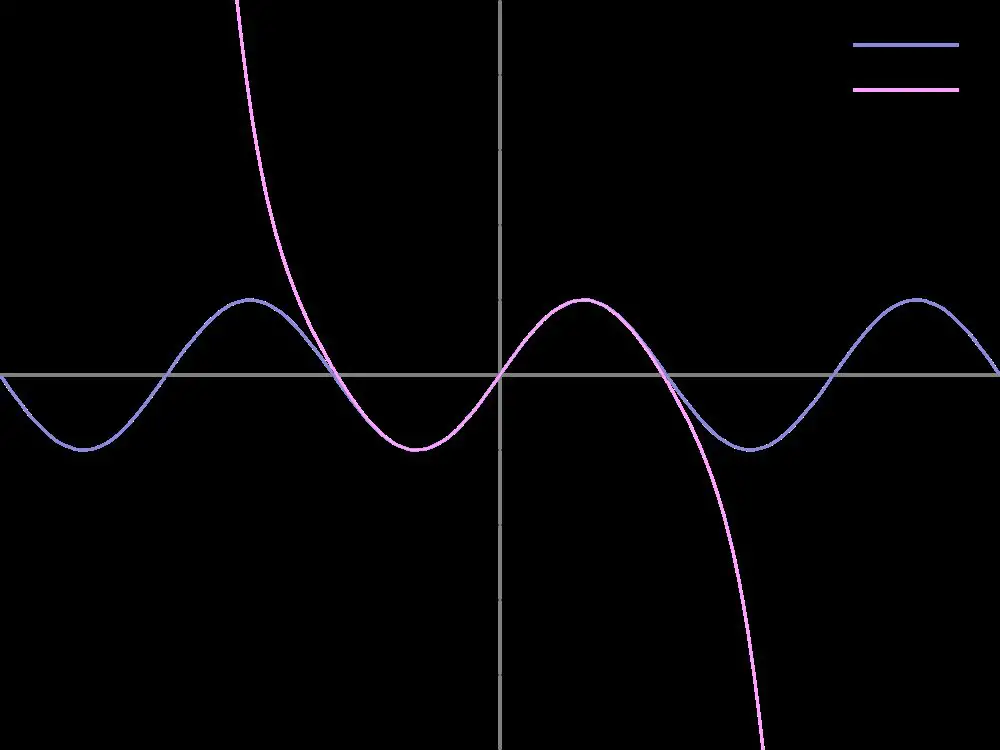
f(a)+ \frac (x-a)
+ \frac (x-a)^2 + \ldots + \frac(a)} (x-a)^n + \ldots
= \sum_^\infty \frac(a)} (x-a)^n


a = 0 için Taylor formülü basit bir şekil alır, bu özel seriye ``MacLaurin serisi`` denir.



Eğer seri belirtilen aralıktaki her x noktasında f(x)`e yakınsıyorsa f(x) analitik bir fonksiyon olarak adlandırılır. Her sonsuz türevlenebilir fonksiyon analitik değildir. Örneğin, ``f``(``x``) =e −1/``x``², ``x a‰  0`` ve f(0)=0 fonksiyonunun Taylor serisi sıfıra denktir ancak fonksiyonun kendisi sıfırdan farklıdır.

Taylor serileri, fonksiyonların (ör. logaritma) verilen bir noktadaki sayisal değerlerini bulmak için kullanılabilirler. Buna ek olarak, Taylor serileri üzerinden cebirsel işlemler yapmak ör. türev ya da integral almak daha kolay olabilmektedir.

Kaynaklar

Vikipedi

İlgili konular

logaritma matematik türev i̇ntegral analitik fonksiyon

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Taylor serisi Resimleri

Laurent serisi
3 yıl önce

Laurent serisi ("Loran serisi" diye okunur) bu fonksiyonun negatif dereceli terimler de içeren kuvvet serisi temsilidir. Karmaşık fonksiyonların Taylor serileri...
Kuvvet serisi
3 yıl önce

fonksiyonun Taylor serisi olarak karşımıza çıkmaktadır. c 'nin 0 olduğu da oldukça fazladır ki bu durumların en yaygın örneği ise Maclaurin serisidir. O zaman...
Kesme hatası
6 yıl önce

hatası denir. Örneğin, bir f ( x ) {\displaystyle f(x)} fonksiyonunu Taylor serisi ile ele alalım. Her dereceden türevli, gerçek ya da karmaşık bir f (...
Taylor Lautner
3 yıl önce

romanlarından uyarlanan Alacakaranlık Efsanesi film serisindeki Jacob Black rolüyle tanınır. Taylor Lautner, 11 Şubat 1992 tarihinde, Grand Rapids, Michigan...
Legendre chi fonksiyonu
6 yıl önce

Matematikte bir Taylor serisi olan özel fonksiyon Legendre chi fonksiyonu aynı zamanda bir Dirichlet serisidir. χ ν ( z ) = ∑ k = 0 ∞ z 2 k + 1 ( 2 k +...
Brook Taylor
6 yıl önce

Brook Taylor FRS (18 Ağustos 1685 – 29 Aralık 1731), en çok Taylor teoremini ve matematiksel analizde kullanımları için önemli olan Taylor serisini yaratmasıyla...
Kuvvet fonksiyonu
3 yıl önce

kuvvetlerine göre adlandırılır. Bir kuvvet fonksiyonunun Taylor serisi, genellikle bir kuvvet serisidir. İyi bilinen aritmetik fonksiyonların Bell serisinde...
Özdeşlik teoremi
6 yıl önce

göstermektir. Bir holomorf fonksiyon kendi tanım kümesindeki her yerde kendi Taylor serisi vasıtasıyla temsil edilebildiği için S = { z ∈ D | f ( k ) ( z ) = g...