Türkçe Bilgi logo TürkçeBilgi

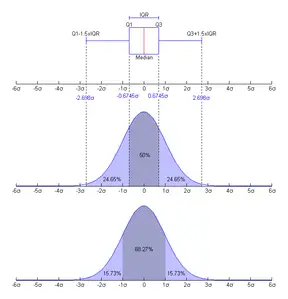
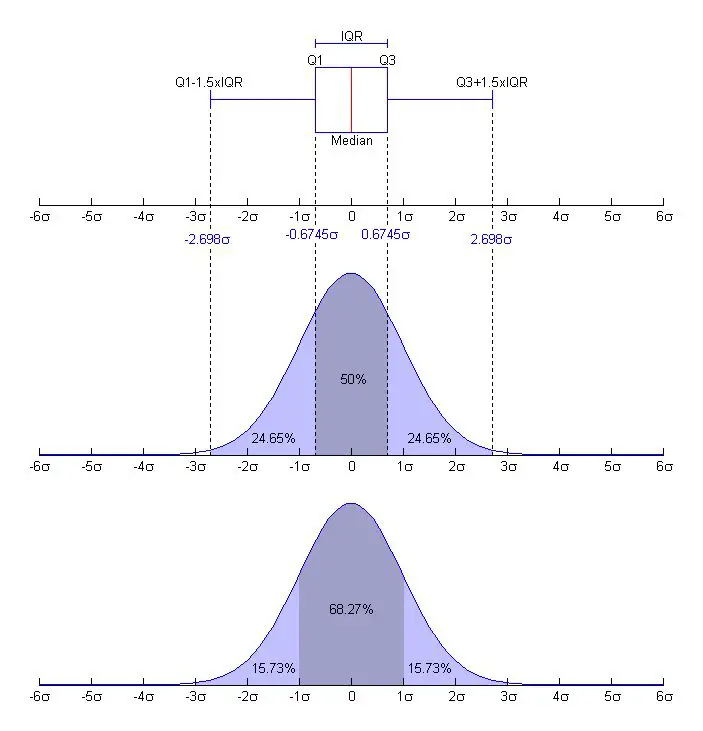
Çeyrekler Açıklığı

Kısaca: Betimsel istatistikde çeyrekler açıklığı sıralanmış bir veri dizisinin orta yarısını (%50sini) kapsayan ve üçüncü dörttebirlik ve birinci dörttebirlik aralığını veya farkını (yani Q3 - Q1) gösteren bir istatistiksel yayılma ölçüsüdür. Birinci dörttebirlik sıralanmış veri dizisinin ilk %25inden büyük ve üçüncü dörttebirlik sıralanmış veri dizisinin %25inden daha küçük olduğu için, bu iki dörttebirlik arasında kalan veri yüzdesi %50dir. ...devamı ☟

Çeyrekler açıklığı
Çeyrekler Açıklığı

Betimsel istatistikde çeyrekler açıklığı sıralanmış bir veri dizisinin orta yarısını (%50sini) kapsayan ve üçüncü dörttebirlik ve birinci dörttebirlik aralığını veya farkını (yani Q3 - Q1) gösteren bir istatistiksel yayılma ölçüsüdür. Birinci dörttebirlik sıralanmış veri dizisinin ilk %25inden büyük ve üçüncü dörttebirlik sıralanmış veri dizisinin %25inden daha küçük olduğu için, bu iki dörttebirlik arasında kalan veri yüzdesi %50dir. Çeyrekler açıklığı ölçüm birimi veri ölçüm birimi ile aynıdır. Çeyrekler açıklığı sıralanmış veriler içinde aşırı küçük veya aşırı büyük uçsal değerlerden (yani dışlak değerlerden) etkilenmez. Özel bir istatistiksel terimle Çeyrekler açıklığı güçlü (en:robust) bir yayılma ölçüsüdür. Bu nedenle istatistiksel yayılma ölçüsü olarak açıklık'a tercih edilir. Eğer alışılagelen yayılma ölçüsü olarak genellikle kullanılan varyans veya standart sapma için mevcut olduğu bilinen dezavantajlar pratik bir problem için sorun yaratıyorsa (örnegin veri dizisi içinde çok aşırı bir veya birkaç dışlak değer varsa) çeyrekler açıklığı varyans veya standart sapma ya da tercih edilir. Çeyrekler açıklığı ölçümü Şu örnek veri serisi için veriler sıralanmış ve beraberlik olan 75 icin 1234 sıralama stratejisi uygulanarak sıralama düzeni bulunmuştur: Örnek: Sıralama düzeni Sıralı veri dizisi 10 15 23 38 42 55 57 59 67 71 71 75 75 79 Bu örnek için açıklık 79-10=69 olur. Medyan değeri sıra numarası ½(14+1)=7,5 yani 07 ve 08 sıra numaralı veriler tam ortasında olup 58dir. Birinci dörttebirlik (Q1) ¼ (14+1) = 3,75 sıra numarali olup 3 sıra numaralı veriye 3 ile 4 sıra numaralı veriler arasındaki aralığın 0,75nin eklenmesi ile elde edilir: :Q1 = 23 + 0,75 (38-23) = 34,25 olur Üçüncü dörttebirlik (Q3) (3/4)(14+1)= 11,25 sıra numaralı olup 11 sıra numaralı veriye 11 ile 12 sıra numaralı veriler arasındaki aralığın 0,25nin eklenmesi ile elde edilir: :Q3 = 71 + 0,25 (75-71) = 72 olur Böylece çeyrekler açıklığı Q3- Q1 = 72 - 34,25 = 37,75 olarak bulunur. Olasılık dağılımları için çeyrekler açıklığı Bir sürekli olasılık dağılımı için, cebirsel olarak, olasılık yoğunluk fonksiyonunun negatif sonsuz (-aˆž) değerden 0,25 değere kadar bulunan integral değeri birinci dörttebirliği; ve yine negatif sonsuzdan (-aˆž) 0,75 değere kadar alınan integral ise üçüncü dörttebirliği verir. Ancak birçok sürekli olasılık dağılımı için olasılik yoğunluk fonksiyonunun integralini almak çok zor olduğu, hatta bazı çok kullanılan dağılımlar için (ornegin normal dağılım) imkansız olduğu bilinmektedir. Eğer gösterim çok iyi ve uygun ölçekli yapılmış ise, gösterimsel olarak da yığmalı olasılık dağılımi eğrisi üzerinde dörttebirlikler hemen bulunabilir. Bazı olasılık dağılımları için çeyrekler açıklığı ve medyan değerleri şöyle verilebilir:

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Çeyrekler açıklığı Resimleri

Açıklık (istatistik)
3 yıl önce

uygun bir istatistiksel yayılım ölçüsü olarak çeyrekler açıklığı kullanılması tavsiye edilir. Açıklık ortası noktası en küçük ve en büyük uçsal noktaların...
Dörttebirlik
3 yıl önce

arasındaki fark bir yayılım ölçüsü olarak kullanılıp, çeyrekler açıklığı veya dörttebirlikler açıklığı' diye anılır. Önce veriler sıralama düzenine koyulur...
Kutu grafiği
7 yıl önce

Verinin yayılmasının açıklık ölçüsüyle ölçülen niteliği, "kutu grafiği"'nin (yatay veya dikey) tüm çizgisi ile görülür. Çeyrekler açıklığı ise "kutu grafiği"nde...
Betimsel istatistik
3 yıl önce

Medyan Mod Kesirlilikler (kantil) İstatistiksel yayılma ve sapma Çeyrekler açıklığı Açıklık Standart sapma, varyans ve varyasyon katsayısı Çarpıklık ölçüsü...
Çoklu sayılı özetleme tabloları
7 yıl önce

özetlenmekte; minimum ve maksimum verilmekle açıklık değeri ve dörttebirlikler verilmekle çeyrekler açıklığı açıkça görülüp çokluluk dağılımının istatistiksel...
Lockheed C-5 Galaxy
7 yıl önce

Özellikleri: En yüksek hız: 855 ;km /sa Düz uçuş hızı: 919 km /sa Kanat açıklığı: 68 m (her bir kanat bir basketbol sahasından daha büyüktür.) Menzil: 12...
Ölçülme ölçeği
7 yıl önce

İstatistiksel yayılım ölçüsü sadece farklar ve ortalama almayı kapsayan açıklık, çeyrekler açıklığı veya (farkların oranı anlamlı olduğu için) standart sapma olabilir...
Stephane Lasme
3 yıl önce

olan Lasme pivot ve uzun forvet pozisyonlarında görev almaktadır. Kanat açıklığı 2 metre 20 santimdir. Savunmacı kimliği ile ön plana çıkmaktadır.Galatasaraylı...