Ortak Çarpan Parantezine Alma
"4x-10" işleminde her iki terimde de 2 çarpanı vardır. Bu işlem "2(2x-5)" şeklinde yazılabilir. Yani:4x-10=2(2x-5)
Gruplandırma
a3-2a2+2a-4 işleminde, ilk iki terim ile son iki terimde sırasıyla a2 ve 2 çarpanları vardır. Yani bu şekilde ayrı ayrı çarpanlara ayrılırsa:a3-2a2+2a-4=a2(a-2)+2(a-2) olur.
Daha sonra oluşan işlemde a-2 çarpanları görülür ve ortak çarpan parantezine alınabilir:
a2(a-2)+2(a-2)=(a-2)(a2
x³-x2+x-1 çarpanlarına ayırırken,
x2(x-1)+1(x-1),daha sonra ortak olan çarpanları bi
tarafa kalanları bi tarafa alırız, (x2+1)(x-1) olarak alınır..
Tam Kare İfadeleri Çarpanlarına Ayırma
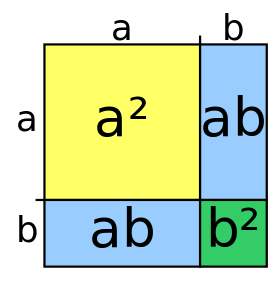
(a+b)2 şeklindeki ifadeleri ayırmak için şu yöntem kullanılır:Önce birinci terim (örnekte a)`in karesi yazılır. Daha sonra aradaki işaret konulur (örnekte pozitif). Ardından her iki terimin çarpımının iki katı alınır (örnekte 2.a.b=2ab). Ardından da artı işareti konulur ve ikinci terimin karesi alınarak (örnekte b) işlem tamamlanır. Yani:
(a+b)2=a2+2ab+b2
(a-b)2si alınırken önce birinci terimin karesi alınır daha sonra,iki sayı çarpılıp ikikatı alınır(işaret - alınır),son olarak ikincinin karesi alınır..
(a-b)2=a2-2ab+b2
İki Kare Farkı
Adından da anlaşılacağı gibi, bu ifadeler a2-b2 şeklindedir. Şu şekilde ayrılır: İlk terimin kareköküyle ikinci terimin karekökü bir toplanır bir çıkartılır. Yani:a2-b2=(a+b)(a-b)