Mutlak değer fonksiyonunun gerçel sayılarla kullanımı dışında, geniş bir matematiksel kullanım alanı vardır. Örneğin, mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir.
Gerçel sayılar
Her gerçel sayısının mutlak değeri şeklinde ifade edilir ve şu şekilde tanımlanır:Yukarıda da görüldüğü gibi `nın mutlak değeri ya artı ya da sıfır değerini alacak, hiçbir zaman eksi değeri almayacaktır.
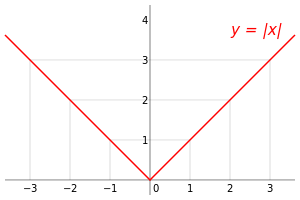
Geometrik anlamda, bir gerçel sayının mutlak değeri onun sayı doğrusunda sıfıra olan uzaklığıdır. Daha genel anlamdaysa mutlak değer iki reel sayı arasındaki farkı, sayı doğrusunda aralarındaki uzaklık olarak verir.
Aşağıdaki yordamlar bir mutlak değerin çözümünde yardımcı olabilecek önermeler içerir.
1. ÖNERME:
2. ÖNERME:
Mutlak değer aşağıdaki dört temel özelliğe sahiptir:
{| cellpadding=10
|-
|
|Negatif olmama
|-
|
|Sıfır eşitliği
|-
|
|Çarpanlara ayrılabilme
|-
|
|Schwarz Eşitsizliği
|}
3. ÖNERME:
Mutlak değerin diğer önemli özellikleri ise:
{| cellpadding=10
|-
|
|Simetri
|-
|
|a ve b eştir
|-
|
|Üçgen eşitsizliği
|-
|
|Bölmenin ayrılması (çarpanlara ayrılabilirlik gibi)
|-
|
|(Alt toplananlara ayrılabilirlik)
|}
Diğer iki kullanışlı eşitsizlikler ise:
Aşağıdakilerse genelde eşitsizlik çözümünde kullanılır; örneğin:
{|
|-
|
|
|-
|
|
|}
Karmaşık sayılar
Karmaşık sayılara kadar olan kısımda, verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1`i ele alırsak: her gerçel sayının bir karmaşık sayı olduğunu ve,
bir karmaşık sayının
olduğunu düşünürsek göreceğiz ki, gerçel sayılarda y katsayısı 0`a eşit. Öyleyse gerçekte `nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir.
Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz:
Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki gibi iki sayının farkının mutlak değerini alırız.
Karmaşık sayılar yukarıda verilen 2. ve 3. önermelerin tüm özelliklerini taşır. Bununla beraber,
ise, ve
z karmaşık sayısının eşlenik`i ise, açıkça görülür ki:
