Türkçe Bilgi logo TürkçeBilgi

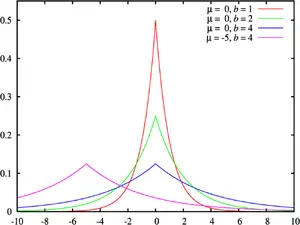
Laplace Dağılımı

Kısaca: Laplace dağılımı Pierre-Simon Laplace anısına isimlendirilmiş bir sürekli olasılık dağılımıdır. Arka arkaya birbiriyle yapıştırılmış şekilde ve bir de konum parametresi dahil edilerek birleştirilmiş iki üstel dağılımdan oluştuğu için, çift üstel dağılımı adı ile de anılmaktadır. İki bağımsız ve tıpatıp aynı şekilde üstel dağılım gösteren bir rassal değişken bir Laplace dağılımı ile işlev görürler. Bu, aynen üstel dağılım gösteren rassal zamanda değerlendirilen Brown devinimine benzer. ...devamı ☟

Laplace dağılımı
Laplace Dağılımı

Laplace dağılımı Pierre-Simon Laplace anısına isimlendirilmiş bir sürekli olasılık dağılımıdır. Arka arkaya birbiriyle yapıştırılmış şekilde ve bir de konum parametresi dahil edilerek birleştirilmiş iki üstel dağılımdan oluştuğu için, çift üstel dağılımı adı ile de anılmaktadır. İki bağımsız ve tıpatıp aynı şekilde üstel dağılım gösteren bir rassal değişken bir Laplace dağılımı ile işlev görürler. Bu, aynen üstel dağılım gösteren rassal zamanda değerlendirilen Brown devinimine benzer. Karekteristikler

Olasılık yoğunluk fonksiyonu

Eğer bir rassal değişken şu olasılık yoğunluk fonksiyonu gösteriyorsa, o rassal değişken bir Laplace(μ,b) dağılımı gösterir: :f(x|\mu,b) = \frac \exp \left( -\frac \right) \,\! :: = \frac \left\ \exp \left( -\frac \right) & \mboxx < \mu \\[1] \exp \left( -\frac \right) & \mboxx \geq \mu \end\right. Burada, μ konum parametresi ve b > 0 ölçek parametresi olurlar. Eğer μ = 0 ve b = 1, pozitif yarı-doğru tıpatıp 1/2 oran ile ölçeklenmiş bir üstel dağılımdır. Laplace dağılımı icin olasılık yoğunluk fonksiyonu bir normal dağılımı anımsatmaktadır. Fakat normal dağılım ortalama μdan farkın karesi terimleri ile ifade edilirken, buna karşılık Laplace dağılım yoğunluğu ortalamadan mutlak farklar terimleri ile ifade edilmektedirler. Sonuç olarak normal dağılıma nazaran Laplace dağılım daha şişkin kuyruklar gösterir.

Yığmalı dağılım fonksiyonu

(Eğer iki simetrik hal görülüp ayırt edilirlerse), Laplace dağılımının integralinin alınması kolaydır. Çünkü bu işlem için mutlak değer fonksiyonu kullanılır. Böylece yığmalı dağılım fonksiyonu şöyle bulunur: ^x \!\!f(u)\,\mathrmu |- | | = \left\ &\frac12 \exp \left( -\frac \right) & \mboxx < \mu \\[2] 1-\!\!\!\!&\frac12 \exp \left( -\frac \right) & \mboxx \geq \mu \end\right. |- | |=0.5\, + \sgn(x-\mu)\,(1-\exp(-|x-\mu|/b)). |} Ters yığmalı dağılım fonksiyonu şöyle verilir: :F^(p) = \mu - b\,\sgn(p-0.5)\,\ln(1 - 2|p-0.5|). Laplace değişebilirlerinin üretilmesi Bir rassal değişken olan Unun (-1/2,1/2] aralığında bulunan tekdüze dağılımdan çekilmiş olduğu bilinirse, şu değişebilir :X=\mu - b\,\sgn(U)\,\ln(1 - 2|U|) μ ve b parametreleri olan bir Laplace dağılımı gösterir. Bu sonuç yukarıda verilen ters yığmalı dağılım fonksiyonundan hemen çıkartılır. Bir Laplace(0,b) değişebiliri Üstel(1/b) dağılım gösteren iki bağımsız ve aynen dağılım gösteren rassal değişken arasındaki fark olarak üretilebilir. Buna eşit olan bir şekilde, bir Laplace(0,1) değişebiliri, tekdüze dağılım gösteren iki bağımsız ve aynen dağılım gösteren rassal değişkenlerin oranının logaritması olarak üretilebilir. Parametre kestirimi N sayıda bağımsız ve aynı şekilde dağılım gösteren örneklemler x1, x2, ..., xN olarak verilsin, \muun kestirimcisi (yani \hat) olarak örneklem medyanı alınsın, o halde b parametresinin kestirimcisi şu olur: :\hat = \frac \sum_^ |x_i - \hat|, Bu bir maksimum olabilirlilik kestirimcisidir. Momentler :\mu_r' = \bigg(}\bigg) \sum_^r \bigg b^k \mu^ k! \\bigg İlişkili dağılımlar * Eğer X \sim \mathrm(0,b)\, ise, o zaman |X| \sim \mathrm(b^)\, bir üstel dağılım gösterir. * Eğer X \sim \mathrm(\lambda)\, ve X\,den bağımsız olan Y \sim \mathrm(0.5)\, iseler, o halde X(2Y-1) \sim \mathrm (0,\lambda^) \, olur. * Eğer X_1 \sim \mathrm(\lambda_1)\, ve X_1dan bağımsız olan X_2 \sim \mathrm(\lambda_2)\, ise, o halde\lambda_1 X_1-\lambda_2 X_2 \sim \mathrm\left(0,1\right)\, olur ． İç kaynaklar * Log-Laplace dağılımı

Kaynak

*

Notlar

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

Olasılık dağılımı
3 yıl önce

Hiperbolik dağılım Hiperbolik sekant dağılımı Landau dağılımı Laplace dağılımı Lévy çarpık alpha-durağan dağılımı: Çok kere finansal verileri ve kritik...
Laplace denklemi
3 yıl önce

Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri...
Normal Dağılım
3 yıl önce

geliştirilmiştir ve bu sonuç şimdi de Moivre-Laplace teoremi olarak isimlendirilmektedir. Laplace normal dağılımı incelemkte olduğu deneylemelerde hataların...

Normal Dağılım, Karl Friedrich Gauss, Rassal değişken, Yoğunluk fonksiyonu, Hipergeometrik dağılım, Pierre Simon Laplace, Abraham de Moivre
Üstel dağılım
3 yıl önce

{\displaystyle Y=X_{1}-X_{2}\,} ise Y ∼ Laplace {\displaystyle Y\sim \operatorname {Laplace} } olur yani Y Laplace dağılımı gösterir. Bağımsız üstel dağılımlar...

Üstel dağılım, Olasılık Dağılımları, Basıklık, Bağımsızlık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu
Student'in t dağılımı
3 yıl önce

bilim dallarında t-dağılımı ya da Student'in t dağılımı genel olarak örneklem sayısı veya sayıları küçük ise ve anakütle normal dağılım gösterdiği varsayılırsa...

Student`in t dağılımı, Olasılık Dağılımları, Basıklık, Beklenen değer, Benford`un savı, Bernoulli dağılımı, Beta dağılımı, Binom dağılımı, Bozulmuş dağılım, Dirac delta fonksiyonu, Dublin
Pareto Dağılımı
3 yıl önce

kullanılmıştır. İktisat bilim dalı dışında bu dağılım Bradford dağılımı adı altında da bilinmektedir. Pareto dağılımı iktisat dışında, sosyal bilimler, fen,...
Bernoulli dağılımı
3 yıl önce

ayrık olasılık dağılımıdır. İsmi ilk açıklamayı yapan İsviçreli bilim adamı Jakob Bernoulli anısına verilmiştir. Eğer X Bernoulli dağılımı gösteren bir...

Bernoulli dağılımı, Olasılık Dağılımları, İstatistik, Aralıklı olasılık dağılımı, Basıklık, Beklenen değer, Benford`un savı, Beta dağılımı, Binom dağılım, Binom dağılımı, Bozulmuş dağılım
Genelleştirilmiş Pareto Dağılımı
6 yıl önce

Pareto dağılımı ailesi, olasılık kuramı ve istatistik bilim dallarında geliştirilen ve özellikle iktisat incelemelerinde gelir ve servet dağılımı analizi...