Bir faz uzayında, her serbestlik derecesi ve ya sistem değişkeni çok boyutlu bir uzayda bir eksen olarak gösterilir. Sistemin olası her durumu için, ve ya sistem değişkenlerinin değerlerinin izin verilen kombinasyonları için, çok boyutlu uzayda bir nokta işaretlenir. Bu işaretli noktaların temsili, sistemin durumunun zamana göre ilerlemesiyle benzerdir. Sonunda, faz diyagramı sistemin olabileceği her durumu temsil eder ve diyagramın şekli, aksi halde açık seçik olmayacak, sistemin niteliklerini aydınlatır. Bir faz uzayı bir çok boyuttan oluşabilir. Örneğin, bir çok molekülden oluşan bir gaz ``x``, ``y`` ve ``z`` konumlarındaki herbir parçacığın, konumu, hızı ve diğer başka özellikleri için ayrı bir boyut gerektirebilir.
Klasik mekanikte faz uzayının koordinatları genel koordinatlar qi ve onların konjuge eşlenikleri pi`dir. Bu uzaydaki sistemlerin istatistiksel grubunun hareketi klasik istatistik mekanik tarafından incelenmektedir. Böyle bir sistemdeki noktaların yerel yoğunluğu Liouville teoremine (Hamiltonian) uymaktadır ve böylece sabit olarak alınabilir. Klasik mekanikta bir örnek sistem bağlamında, sistemin verilen herhangi bir zamandaki faz uzayı koordinatları sistemin tüm dinamik değişkenlerinden oluşmaktadır. Bu yüzden, sistemin geçmişte ve ya gelecekteki durumunu hesap etmek, Hamilton`un ve ya Lagrange`ın hareket denkleminin integrasyonuyla mümkündür. Dahası, faz uzayında her bir noktanın kesinlikle bir yörüngede bulunması sebebiyle, hiçbir şekilde faz yörüngeleri kesişmez.
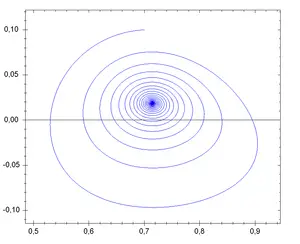
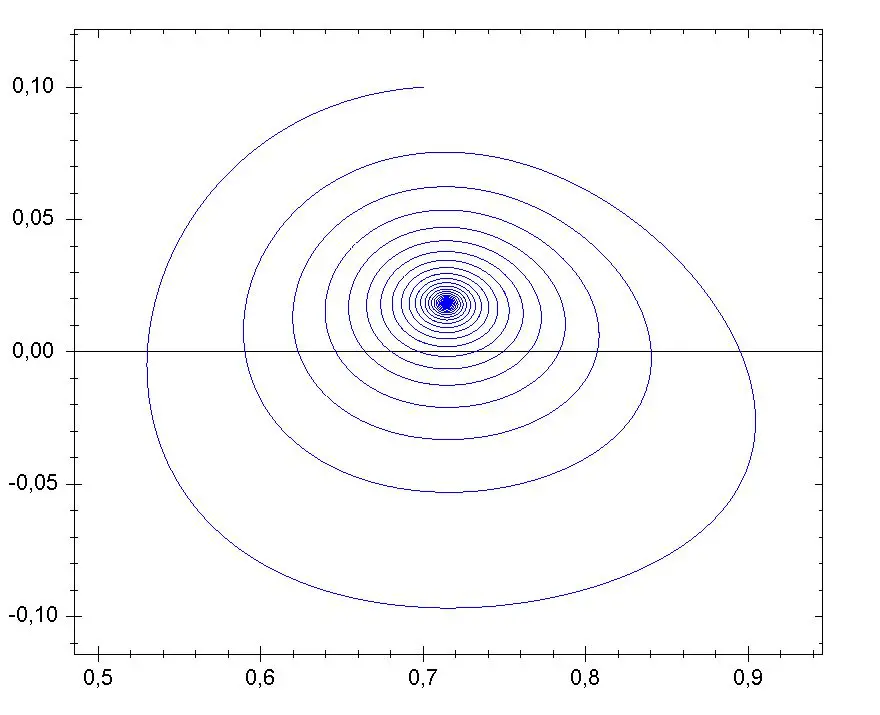
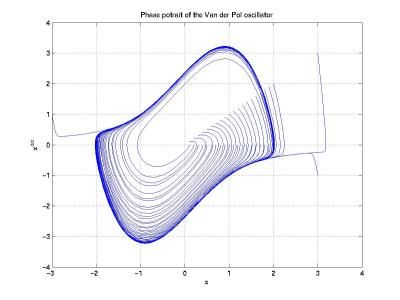
Örneğin tek bir parçacığın bir boyutta hereket ettiği basit sistemlerde, iki serbestlik derecesi kadar az serbestlik derecesi olabilir, (tipik olarak, konum ve hız), ve faz tasvirinin bir krokisi sistemin dinamiği ile ilgili niteliksel bilgi verebilir, diyagramda gösterilen Van der Pol osilatörünün sınır-döngüsü gibi.
Burada, yatay eksen konumu ve dikey eksende hızı verir. Sistem ilerledikçe, durumu faz diyagramındaki eksenlerden birini izler.
Kaos teorisinden klasik bir faz diyagramı örneği de "Lorenz attractor"ü ve "Mandelbrot set"idir.
Kuantum mekaniği
Kuantum mekaniğinde, faz uzayının ``p`` ve ``q`` koordinatları bir Hilbert uzayındaki hermitian opetaörlere dönüşürler, fakat alternatif olarak kendi klasik yorumlamalarını da kaybetmezler, bunların sağlanan fonksiyonları yeni cebirsel yollar oluştururlar(Moyal çarpımı, Groenewold`un 1946 yıldız çarpımı).Her bir kuantum mekaniği observable`ı faz uzayında tek bir eşsiz fonksiyona ve ya dağılıma uyar ve Hermann Weyl tarafından belirtildiği (1927) ve John von Neumann (1931); Eugene Wigner (1932); H J Groenewold (1946) tarafından bunların büyük bir sentezinde belirtildiği gibi tersi de doğrudur.
Josí© Enrique Moyal (1949) ile, bunlar kuantum mekaniğinin mantıksal otonom bir reformülasyonu olan faz-uzayı nicelemesini tamamlamıştır.Deformasyon nicelemesi ve geometrik niceleme bunun modern soyutlamalarındandır.
Termodinamik ve istatistiksel mekanik
Termodinamikte ve istatistiksel mekanik bağlamında, faz uzayının iki anlamı vardır:- Klasik mekanikte olduğuyla aynı şekilde kullanılmaktadır.Eğer bir termodinamik sistem N parçacıkdan oluşuyorsa, 6N boyutsal faz uzayındaki bir nokta o sistemdeki herbir parçacığın dinamik durumunu gösterir. Aynı şekilde, faz uzayındaki bir noktanın sistemin mikro durumu olduğu söylenir. ``N`` tipik olarak Avagadro sayısının tertibindedir, bu yüzden mikroskopik seviyedeki bir sistemi tanımlamak genellikle pratik değildir. Bu ise bizi faz uzayının farklı bir şekilde kullanımına yönlendirir.
- Faz uzayı sistemin parametrelerinin basınç, sıcaklık gibi makroskopik durumlarından oluştuğu bir uzayı anlatır. Örneğin, basınç-hacim ve ya entropi-sıcaklık diyagramının bu faz uzayının bir kısmını betimlediğini söyleyebiliriz. Bu faz uzayındaki bir nokta aynı şekilde makro durum olarak adlandırılır. Aynı makro durumda birden fazla mikro durum olabilir. Örneğin sabit bir sıcaklıkta, sistem mikroskopik seviyede birçok dinamik konfigürasyona sahip olabilir. Bu şekilde kullanıldığında, bir faz değişimi faz uzayının bir bölgesidir, ki bu uzayda konu edilen sistem sıvı ve ya katı fazdadır.
Makro durumlardan daha fazla mikro durum bulunduğundan, ilk durumdaki faz uzayı genellikle ikinci durumdakilerden daha büyük boyutlardaki bir manifolddur. Açık şekilde, sistemin; moleküllerden ve ya atomik düzeyden sıcaklık ve ya sistem basıncına kadar her detayını kaydetmek için daha fazla değişken gerekmektedir.
Kaynakça
- kaynak wiki |url=http://en.wikipedia.org/wiki/Phase_space | tarih=28 Ağustos 2007 | dil=İngilizce | madde=Phase space