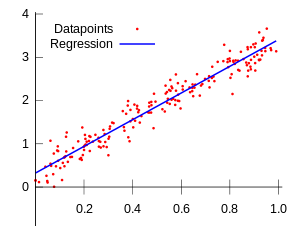
Çizgisel örnek
ile bulunmuş teorik bağlantıyı ifade eder.]Basit bir örnek vermek gerekirse, aralarında çizgisel (lineer) bir bağlantı olan, ``X`` ve ``Y`` adında iki fiziksel büyüklük düşünelim. (Mesela, ``X`` belli bir ağaç türünün yaşı, ``Y`` aynı tür ağacın gövde çapı olabilir.) ``Y`` `yi ``X`` `in fonksiyonu olarak yazmak istiyoruz. Bu iki büyüklük arasındaki bağlantı çizgisel olduğuna göre, şöyle bir denklem halinde ifade edilebilir:
Bizim aradığımız şey, bu denklemdeki ``a`` ve ``b`` sayıları için mümkün olan en doğru değerlerdir. Bu değerleri belirlemek için bir dizi ölçüm yaptığımızı düşünelim. (Ağaç örneğine dönersek, ilgilendiğimiz türden pek çok ağacın yaşını ve gövde çapını ölçelim.) Bu ölçümler bize bir dizi (xi, yi) çifti verecektir. Bir kartezyen düzlem üzerinde bu çiftlere karşılık gelen noktaları tek tek işaretlersek, kabaca düz bir çizgi üzerinde yayılmış bir "noktalar bulutu" elde ederiz. Noktalar, çeşitli sebeplerden dolayı (ölçüm hataları, istisnai durumlar, modele katılmayan dış etkiler, vs) kusursuz bir çizgi üzerinde çıkmayacaktır.
``X`` ve ``Y`` arasındaki bağlantıyı tek bir çizgisel denklem olarak ifade etmek istiyorsak, bu noktalara mümkün olduğunca yakın geçecek bir çizgi bulmalıyız. Bir başka deyişle, yukarıdaki denklemde ``a`` ve ``byi öyle seçmeliyiz ki, ortaya çıkan çizgi veri noktalarına mümkün olduğunca yakın olsun.
En küçük kareler yöntemi, denklemin verdiği (teorik) ``Y`` değerleri ile ölçümlerin verdiği (gerçek) ``Y`` değerleri arasındaki farkların ``karelerinin`` toplamını küçültme fikrine dayanır. Bu yöntem, denklemdeki ``a`` ve ``b`` sayılarını, bahsedilen kareler toplamını en küçük yapacak şekilde seçer (ve adını da buradan alır).
Tarihi
Bilindiği kadarıyla, en küçük kareler yöntemi ilk olarak 1795`te Carl Friedrich Gauss tarafından geliştirilmiştir. Gauss 1801 yılında bu yöntemi kullanarak, keşfinden kısa süre sonra kaybedilen Ceres asteroidinin tekrar gözlemlenebileceği pozisyonu hesaplayabilmiş, bu başarısıyla büyük üne kavuşmuştur. Gauss bu yöntemi ilk olarak 1809`da yayımlamıştır. 1806`da Fransız matematikçi Adrien-Marie Legendre ve 1808`de Amerikalı matematikçi Robert Adrain, Gauss`tan (ve muhtemelen birbirlerinden) bağımsız olarak bu yöntemi geliştirip kullanmışlardır.En küçük kareler yöntemi, bugün neredeyse tüm bilim dallarında ve mühendislikte yaygın olarak kullanılmaktadır.
matematik-taslak