Türkçe Bilgi logo TürkçeBilgi

Delta-V

Kısaca: delta-v kavramı tam anlamıyla "hızdaki değişiklik" demek olmasına rağmen belirli bir anlamı vardır: sayıl olup sürat birimlerini alarak bir yörünge manevrası yapabilmek, başka bir ifâdeyle bir rotadan başka bir rotaya geçmek için gerekecek olan "gayreti" hesaplar. ...devamı ☟

Delta-v
Delta-v

delta-v kavramı tam anlamıyla "hızdaki değişiklik" demek olmasına rağmen belirli bir anlamı vardır: sayıl olup sürat birimlerini alarak bir yörünge manevrası yapabilmek, başka bir ifadeyle bir rotadan başka bir rotaya geçmek için gerekecek olan "gayreti" hesaplar. :\Delta = \int_^ }\, dt Burada :T anlık itişi :m anlık kütleyi belirler. Dış kuvvetlerin olmaması ve itişin belli bir yönde uygulanması durumunda formül, şu basitleşmiş şekli alır: : = \int_^ \, dt = | _1 - _0 | Bu da yalın biçimde hız değişikliğidir. Roketler için 'dış kuvvetlerin olmaması' ile genelde atmosfer sürüklemesi ve geriye doğru aerostatik basıncın aracın burnunda olmaması ifade edilir. Bu durum vakum ispin hesaplarda kullanılmasına imkan verir ve delta-v kapasitesi böylece roket denklemiyle hesaplanır. Atmosfer kayıplarının oluşturduğu "masraflar"sa gezegen yüzeyinden kalkışlar hesaplandığında delta-v bütçesine aktarılır. Uçuş yolları için kullanılan delta-v'ler Bir uçuş yolu tasarlandığında delta-v, kullanılacak yakıtın ne kadar olduğunu gösteren bir göstergedir. Yakıt kullanımı, delta-v'nin roket denklemiyle gereğince hesaplanan üslü bir işlevidir. Aracın ilk ve son konumundaki tüm enerjisini kullanarak enerjinin korunumu prensibiyle delta-v ihtiyaçlarını tespit etmek mümkün değildir. Çünkü yakıt yandığında sistemden enerji götürmektedir (aşağı da bakınız). Aynı zamanda yakılan yakıt da yok olmaktadır. Mesela çoğu uzay aracı bir yörüngeye gönderildiğinde uzaya fırlatıldığı yerin enlemine yakın bir eğiklikle hareket ettirilir. Böylece Dünya'nın dönüşünden kaynaklanan yüzeysel hızından yararlanılmış olur. Gerekirse uzay uçuşu görevinden kaynaklanan sebeplerden dolayı uzay aracını bu eğiklikten farklı bir eğiklikle uzaya fırlatılması durumunda ilk ve son yörüngelerdeki potansiyel enerji aynı olmasına rağmen hatırı sayılır ve daha büyük bir delta-v'ye ihtiyaç vardır. Bir rokete itiş kısa ateş darbeleriyle etkidiğinde diğer ivmeyle ilgili kaynaklar ihmal edilebilir olabilir ve hız değişikliğinin büyüklüğü delta-v'ye bakarak basit bir yaklaşımla saptanabilir. Bu durumda etkiyecek tüm delta-v, her ayrık ateş darbesinde gereken delta-v'lerin toplamıyla basit bir şekilde hesaplanabilir. Bu, her ateş darbesinden sonra hızın büyüklüğü ve yönünün çekim etkisiyle mesela eliptik yörüngeye girerken değişmesine rağmen böyledir. Delta-v hesabına örnekler görmek için Hohman transfer yörüngesi, çekimsel katapult ve gezegenlerarası sürat yoluna bakınız. Ayrıca büyük itişlerin çekimsel sürüklemeyi azalttığı da kayda değerdir. Delta-v, aynı zamanda satelitleri gerektiği gibi yörüngede tutmak için gerekli olup itici yörüngesel konumu tutma manevralarında harcanır. Çoğu satelitlere kalkıştan önce konan yakıt sonradan tekrar yakıt tanklarına doldurulamadığından satelite başta yüklenen yakıt miktarı, pekala onun ömrünü belirliyebilmektedir.

Oberth etkisi

Delta-v'nin hız yönünde uygulandığı ve güç göz önüne alındığında her delta-v birimi için kazanılan belirli yörüngesel enerjinin o anlık hıza eşit olduğu görülür. Hem o anki çekimin, hem de oluşturuduğu ivmenin değişmez olduğu bir roket ateşlemesi için her delta-v birimi için kazanılan yörüngesel enerji, ateşlemeden önce ve sonraki hızın ortalam değerine eşittir. Mesela eliptik bir yörüngede bulunan bir yapay uydunun enerjisi yüksek hızda (yani düşük yükseklikte) düşük hıza (yani büyük yüksekliğe) göre daha verimli bir şekilde arttırılabilir. Bu gerçek

Oberth etkisi

olarak bilinir. Ayrıca yörüngesel katapulta bakınız.

Porkchop çizimi

Gezegenlerin zamanla birbirlerine göre değişen konumlarına göre farkı delta-v'ler değişik fırlatılış tarihlerine göre gerekmektedir. Bu durumu aydınlatan ve delta-v'yi zamana karşı değişimini gösteren diyagrama kimi zaman

Porkchop çizimi

 de denir. Bu diagram fırlatış için en uygun zaman aralığını hesaplamaya mümkün kılar. Çünkü uzaya fırlatılış, ancak kullanılan uzay aracının kapasitesi dahilinde olmalıdır. Delta-v oluşması Delta-v, tipik olarak bir roket motorunun itişiyle ya da başka reaksyon motorlarıyla sağlanabilir. Delta-v'nin zaman değişimi motorlarca oluşan ivme büyüklüğü, başka bir ifadeyle itişin tüm araç kütlesine oranıdır. Asıl ivme vektörü, kütle başına itiş kuvvetini çekim vektörü ve cisme etkiyen bütün diğer kuvvetlere ekleyerek bulunur. Gereken toplam delta-v, tasarımın başlangıç safhası için iyi bir başlama noktasıdır. Daha sonra eklenen karmaşalar, tasarımın ileri safhalarında ele alınmak üzere geciktirilir. Roket denklemi, gereken yakıtın artan delta-v'yle dramatik olarak arttığını gösterir. Bu yüzden modern uzay aracı sevk sistemlerinde hatırı sayılır çaba, uzay aracının toplam delta-v'sini azaltma ve büyük delta-v vermeye muktedir uzay araçları tasarlama yönünde harcanmıştır. Delta-v'yi bir itiş sistemiyle arttıramak için şu tedbirler alınmalıdır: * kademe sistemi kullanmak * özgül itici kuvveti arttırmak * kütle oranını düzeltmek Bunun yanı sıra (çeken gök cismine yakınken) itiş düzeyini arttırarak delta-v bazen arttırılabilir. Güneş Sistem etrafındaki Delta-v'ler

Kullanılan kısaltmalar

Ayrıca bakınız * Delta-v bütçesi * Çekim sürüklemesi * Yörüngesel manevra * Uzay gemisi itişi * Özgül itici kuvvet * Tsiolkovsky roket denklemi

Kaynaklar

Kaynaklar

Vikipedi

Bu konuda henüz görüş yok.
Görüş/mesaj gerekli.
Markdown kullanılabilir.

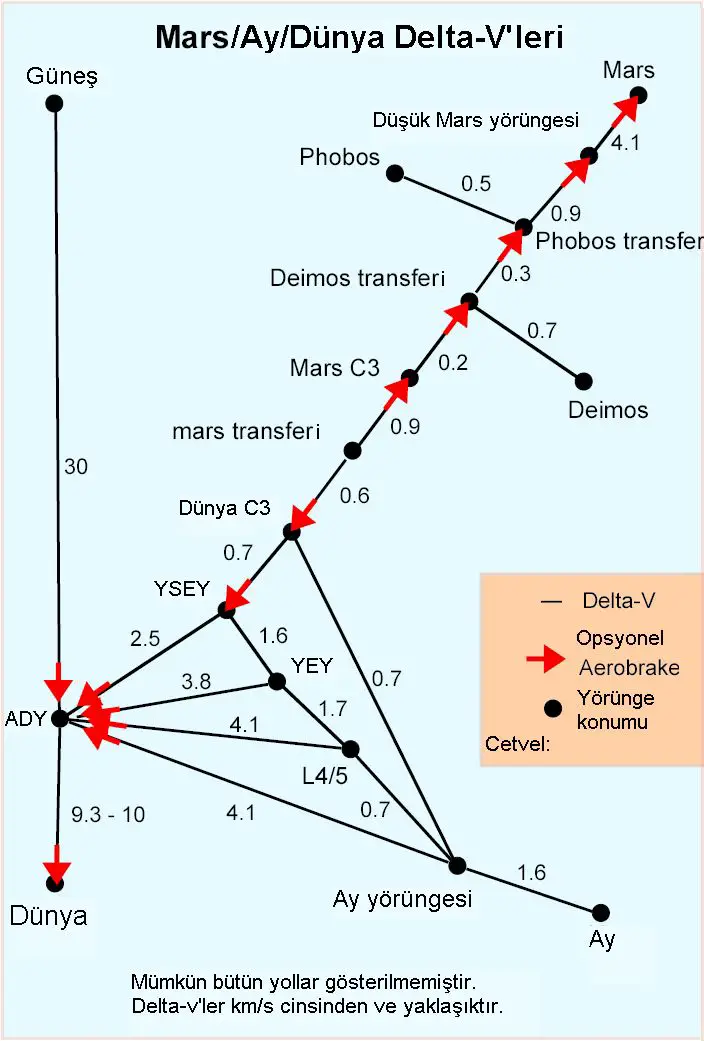
Delta-v Resimleri

Kimyasal enerji
3 yıl önce

= p Δ V {\displaystyle \Delta E=p\Delta V\,\!} , burada entalpi şöyle yazılabilir; Δ H = Δ U + p Δ V {\displaystyle \Delta H=\Delta U+p\Delta V\,\!} ...
Mezarlık yörüngesi
6 yıl önce

(delta-v) çok yüksek olması durumlarında kullanılır. Örneğin Yer istasyonel yörüngelerde bulunan uyduların yörünge değişikliği için 1500 m/s delta-v gerekliyken...
Torricelli denklemi
6 yıl önce

denklemdir. v f 2 = v i 2 ∓ 2 a Δ d {\displaystyle v_{f}^{2}=v_{i}^{2}\mp 2a\Delta d\,} Hız için aşağıdaki eşitliğin olduğunu biliyoruz: v f = v i + a t ...

Torricelli denklemi, Evangelista Torricelli, Klasik mekanik, Taslak, Zaman, İtalyan
Akım Fonksiyonu
6 yıl önce

v + ∂ v ∂ y δ y ) δ x {\displaystyle u\delta y+v\delta x\ =\left(u+{\frac {\partial u}{\partial x}}\delta x\right)\delta y+\left(v+{\frac {\partial v}{\partial...
Delta Scuti
3 yıl önce

Koordinat: 18s 42d 16,427sn; -09º 03' 09,18″ Delta Scuti (δ Sct, δ Scuti), Kalkan takımyıldızı bölgesinde yaklaşık olarak 202 ışık yılı uzaklıkta bulunan...
öteleme
3 yıl önce

T_{\mathbf {\delta } }} şöyle tanımlanır: T δ f ( v ) = f ( v + δ ) . {\displaystyle T_{\mathbf {\delta } }f(\mathbf {v} )=f(\mathbf {v} +\mathbf {\delta } ).}...
Delta Scuti değişeni
6 yıl önce

Delta Scuti değişenleri (δ Scuti), dönemleri 0.3 günden kısa, A veya F tayf türünden, birkaç 0.001 kadirden 0.8 kadire kadar görsel bölge genliklerine...
Hız
3 yıl önce

{\displaystyle (\Delta t)} bölümüyle bulunur. v ¯ = Δ x Δ t . {\displaystyle {\boldsymbol {\bar {v}}}={\frac {\Delta {\boldsymbol {x}}}{\Delta t}}.} Burada...

Hız, Hız