Türkçe Bilgi: Poisson dağılımı

Olasılık dağılımı|

isim    =Poisson|

tip    =kütle|

pdf_image =
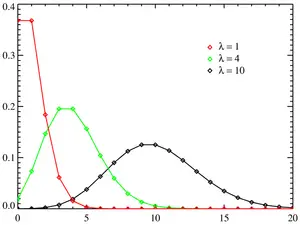
Yatay eksen indeks ``k`` . Fonksiyon yalnızca ``k``nin tamsayı değerleri için geçerlidir. Noktaları bağlayan çizgiler süreklilik göstermez; kullanıcıya yardımcı olmak üzere çizilmişlerdir.|

cdf_image =
Yatay eksen indeks ``k`` .  |

parametreler = $\lambda \in (0,\infty)$ |

destek  = $k \in \$ |ğ

OYF = $\frac \lambda^k}\!$ |

YDF = $\frac\!\textk\ge 0$

(burada

\Gamma(x, y)

Tamamlanmamis gamma fonksiyonu olur)|

ortalama    = $\lambda\,$ |

medyan   = $\text\lfloor\lambda+1/3-0.02/\lambda\rfloor$ |

mod    = $\lfloor\lambda\rfloor$  ve  $\lambda-1$  eğer  $\lambda$  bir tamsayı ise|

varyans  = $\lambda\,$ |

çarpıklık  = $\lambda^\,$ |

basıklık  = $\lambda^\,$ |

entropi  = $\!+\!e^\sum_^\infty \frac$

(büyük

\lambda

değeri için)

\frac\log(2 \pi e \lambda) - \frac - \frac - \frac + O(\frac)

mf    = $\exp(\lambda (e^t-1))\,$ |

kf    = $\exp(\lambda (e^-1))\,$

Olasılık kuramı ve istatistik bilim kollarında, Poisson dağılımı bir aralıklı olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelen sayısının olasığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının sabit olarak bilindiği ve ortalama olay sayısının sabit zaman birimi değişmesi ile aynı oranda değiştiği varsayılır. Ayrica herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkı önceki zaman farklarından bağımsız oluştuğu kabul edilir.

Poisson dağılım çok kere belirli sabit zaman aralığı birimleri bulunan problemlere uygulanmakla beraber diğer birimsel aralıklı problemlere de (yani birim uzaklık, alan veya hacim içeren problemlere de) başarı ile uygulanabilir.

Örnekler

Poisson dağılımı Poisson süreci ile birlikte ortaya çıkar. Poisson süreci aralıklı karakterde olan (yani 0, 1, 2, 3 .. kere meydana çıkan) bazı olgularin bir birim zaman, alan, mekan veya hacimde sabit bir olasılıkla oluşması şekilini alır. Bu çeşit olaylara ve Poisson dağılımının uygulanmasına örnekler şunlardır:

Prusya süvari birliklerinde her bir yıl at ve katır tepmeleri ile ölen asker sayısı: Bu klasik örnek 1868de Ladislaus Josephovich Bortkiewicz tarafından bir kitapta yayınlanmış ve çok tanınmış bir örnek olarak yıllarca askeri ve sivil yüksek okul öğrencilerine verilmiştir.
Bir saat aralığında belli bir Internet sitesine gelen bağlantılar sayısı;
Yarım saat içinde bir nakliyat deposuna yükleme-boşatılma için gelen kamyon sayısı;
Her bir beş dakika içinde bir telefon cevap merkezine gelen telefonlar sayısı;
Belli bir trafik kavşağından 1 dakika içinde geçen otomobil sayısı;
Belli bir zaman aralığında bir büyük binada yanıp çalışması duran florasan lambalarının sayısı;
Bir mucit kişinin çalışma hayatı boyunca patentini aldığı keşifler sayısı;

Birbirini takip eden Poisson tipi olaylar arasındaki aralık karşılıklı ilişkili olarak bir üstel dağılım olur. Örneğin, bir florans ampülünun çalışma süresi veya otobüslerin gelmesi arasındaki bekleme zamanı.

Tarihçe

Bu dağılım ilk defa Simí©on-Denis Poisson (1781–1840) tarafından diğer olasılık hakkındaki yazıları ile birlikte 1838de yayınlanan ``Recherches sur la probabilití© des jugements en matií¨res criminelles et matií¨re civile`` ("Ceza hukuku ve medeni hukuk alanlarındaki hükümlerin olasılığı üzerinde araştırmalar)" adındaki eserinde ortaya atılmıştır.

Nadir olaylar için Poisson dağılımı

Poisson dağılımının genel odaklandığı rassal değişken bir sayılabilen olaydır; bu olay belli bir sabit uzunlukta olan (genellikle zaman) aralıkta aralıklı olarak ortaya çıkar ve bu aralıkta gözlenen olayların sayısı Poisson dağılım için rassal değişkendir. Bu sabit aralıkta ortaya çıkan olaylar sayısının beklenen değeri (ortaya çıkmanın ortalama sayısı) λ olarak sabittir ve bu ortalama değer aralık uzunluğuna orantılıdır. Eğer her 4 dakikalık zaman aralıgı içinde ortalama 5 olay meydan geliyorsa, sabit 8 dakikalık aralıkta ortalama 10 (=4x8/2) olay ortaya çıkar. Herhangi bir negatif olmayan bir tamsayı olan ``k`` sayida (``k``=0, 1,2, 3...) olay ortaya çıkma olasılığı şöyle ifade edilir:

f(k, \lambda)=\frac,\,\!

burada

``e`` bir doğasal logaritmaların bazı (``e`` = 2.71828...)
``k`` olasiligi fonksiyon ile verilmekte olan olayin ortaya cikma sayisi
``k``! ``k`` icin faktoriyel
λ verilen sabit aralikta ortaya cikma sayisinin beklenen degeri; bir pozitif reel sayi.

Bu ``k``nin fonksiyonu Poisson dağılım için olasılık kütle fonksiyonu olur.

Poisson dağılımı için λ parameteresi yalnızca beklenen değer, yani ortaya çıkan

\scriptstyle\langle k \rangle

sayıda olay için bir ortalama, değildir. Aynı zamanda

\scriptstyle\sigma_k^2 \ \stackrel\  \langle k^ \rangle - \langle k \rangle^

yani varyans da olur. Böylece gözlenen olay meydan çıkış sayısı bir ortalama değer λ ile bir standart sapmasi

\scriptstyle\sigma_\, =\, \sqrt

olması özelliklerle bir olasılık dağılım, Poisson dağılımı, göstermektedir.

Genellikle bir Poisson dağılımı büyük sayıda olay ortaya çıkabilmesi mumkun olduğu, ama bu ortaya çıkması mümkün olayların nadir olduğu kabul edilen, sistemlerde uygulanabilir. Bilimsel alanlarda klasik örnekler atomların nükleer parçalanması; verilen bir DNA zincirinde ortaya çıkan mutasyon sayısı vb. Bu orneklerle ve diğer birçok örneğin için, ortaya çıkan nadir olay sayısı aralıklı denemelerin sonucudur ve daha kesinlikle bir binom dağılım kullanılarak model haline getirebilinirler. Fakat ``n`` ve λ/``n`` parametreli bir binom dağılımı (yani her deneme için λ/``n`` başari olasılığı olan ``n`` sayıda deneme için belirli bir başarı sayısı için olasılık dağılımı), deneme sayısı ``n`` büyüyüp limitte sonsuzluğa yaklaştıkça, beklenen değeri λ olan bir Poisson dağılıma yakınlaşır. Bu limit bazan ``nadir olaylar kuralı`` olarak anılmaktadır. Bu ifade bir bakıma yanıltıcıdır; çünkü birçok Poisson dağılımı ile modellenebilen olaylar arasında birçoğu (örneğin bir otobüs durağına yarım saat aralığında gelen otobüs sayısı; bir mobil telefona bir saat aralığında gelen çağrı sayısı gibi) hiç de nadir olmayan olaylar bulunur. Ancak binom dağılımının büyük sayılar için hesaplanması faktoriyel sayılar kullanılmasi gerektirdiği için bu uzun hesaplama biraz sıkıcı görülebilmekte ve bu nedenle Poisson dağılımı yaklaşık olarak binom dağılım yerine kullanılmaktadır.

Binom dağılımından limitte Poisson dağılım olasılık kütle fonksiyonunun çıkartılması matemetiksel ayrıntıları şöyle yapılır:

Önce, degiskenler hesabı (calculus) içinde kullanılan limit şöyle ifade edildiğı hatırlanır:

\lim_\left(1-\right)^n=e^.

Şu eşitlik ``p`` = Î»/``n`` bu ifade içine konulursa, şu denkleme varılır:

\lim_ \Pr(X=k)=\lim_ p^k (1-p)^

=\lim_ \left(\right)^k \left(1-\right)^

ve şimdi bu ifadeyi daha açısın:

=\lim_ \underbrace\right)\left(\right)\left(\right) \cdots \left(\right)}\ \underbrace\right)}\ \underbrace\right)^n}\ \underbrace\right)^{-k

Limitte ``n`` aˆ değere yaklaştıkca, ilk parantez içindeki ifade 1 e yaklaşır ve ikinci parantez içinde ``n`` olmaması nedeniyle sabit kalır; üçüncü parantez içindeki ifade ``e``^−Î» değerine yaklaşır ve dördüncü parntezdeki ifade 1 e yaklaşım gösterir. Sonuçta, limitte şu ortaya çıkar:

\over k!}.\,\!

Daha genel olarak, ``n`` ve ``p``_``n`` parametreleri olan binom rassal değiskenler için bir sıra Binom ifadesi

\lim_ np_n = \lambda,

olursa, bu seri dağılımda ortalaması λ olan bir Poisson rassal değişkeni için serilere yaklaşır (Daha fazla ayrıntı için nadir olaylar kuralı maddesine bakınız.).

Özellikler

Bir Poisson dağılımı gosteren rassal degisken icin beklenen deger e esittir; ve varyans degeri de λdir. Poisson dağılımınin yuksek momentleri λ terimleri ile olusan (matematiksel kombinatorik kuraminda anlamli olan katsayilari bulunan) Touchard polinomlaridir. Eger Poisson dağılımı icin beklenen deger ``1`` ise, o zaman Dobinski`nin formulune gore ``n``inci moment ``n`` buyuklugunde olan set bolunumlerinin sayisina esittir.

Tam sayili olmayan bir Î» lambda parametreli Poisson dağılımı gosteren bir rassal degiskenin mod degeri, Î» degerinin hemen altinda bulunan en yuksek pozitif tamsayi olan $\scriptstyle\lfloor \lambda \rfloor$ ifadesine esittir.

Poisson dağılımı gosteren rassal degiskenlerin toplami:

Eger

X_i \sim \mathrm(\lambda_i)\,

ifadesi

\lambda_i

parametresi ile Poisson dağılımı gosteriyor ve

X_i

terimleri bagimsiz iseler, o zaman

Y = \sum_^N X_i \sim \mathrm\left(\sum_^N \lambda_i\right)\,

ifadesi de parametresi toplama katilan parametre toplamlarindan olusan bir Poisson dağılımı gosterir.

Beklenen degeri λ olan Poisson dağılımınin moment uretici fonksiyonu su ifade ile verilir:

\mathrm\left(e^\right)=\sum_^\infty e^ f(k;\lambda)=\sum_^\infty e^  \over k!} =e^.

Poisson dağılımı icin tum kumulantlar beklenen deger olan λya esittirler. Poisson dagilimi icin ``n``inci moment Î»^``n`` olur

Poisson dağılımlari sonzuz olarak bolunebilir olasilik dağılımlaridir.

Poi(Î»₀) ile Poi(Î») arasindaki yonlendirilmis Kullback-Leibler ayrilimi soyle ifade edilir;

\Delta(\lambda||\lambda_0) = \lambda \left(1 - \frac + \frac \log \frac \right).

Poisson dağılımı ile üretilen rassal değişkenlerin simulasyonu

Poisson dağılımı ile üretilmiş rassal sayıların bir komputer programı ile simulasyonu için algoritma en basit olarak Knuth verilmiştir

algoritma ``poisson rassal sayı üretimi (Knuth)``:

  init:

    Let L a† ``e``^&minus;Î», k a† 0 and p a† 1.

do:

    k a† k + 1.

    [2] aralığı içinde birörnek dağılımlı rassal sayı u üret ve let p a† p í— u.

  while p a‰¥ L.

  return k &minus; 1.

Basit olmakla beraber, karmaşıklık Î» ile doğrusal olarak oranlıdır. Bu sorun etkisini azaltmak için çeşitli diğer algoritmalar geliştirilmiştir (bakın Ahrens ve Dieter).

İlişkili dağılımlar

Eğer

X_1 \sim \mathrm(\lambda_1)\,

X_2 \sim \mathrm(\lambda_2)\,

ise, o zaman

Y = X_1 - X_2

farkı bir Skellam dağılımı gösterir.

Eğer

X_1 \sim \mathrm(\lambda_1)\,

X_2 \sim \mathrm(\lambda_2)\,

bağımsızsalar ve

Y = X_1 + X_2

ise, o zaman

Y=y

ya kosullu

X_1

dağılımı bir binom dağılımı olur. Özellikle,

X_1|(Y=y) \sim \mathrm(y, \lambda_1/(\lambda_1+\lambda_2))\,

olur. Daha genel olarak, eğer

``X``₁, ``X``₂,..., ``X``_``n``
rassal değişkenleri, parametreleri

Î»₁, Î»₂,..., Î»_``n``
olan Poisson dağılımı gösteriyorlarsa, o zaman

X_i \left|\sum_^nX_j\right.\sim\mathrm\left(\sum_^nX_j,\frac^n\lambda_j}\right)

Eğer denemeler sayısı limitte sonsuza doğru yaklaşır ve başarı sayısının değer]i sabit kalırsa, bu binom dağılım limitte Poisson dağılıma yaklaşacağı isbat edilmiştir. Bu nedenle Poisson dağılım, eğer ``n`` yeterce büyük ve ``p`` yeterce küçük ise, bir binom dağılım yerine yaklaşım olarak kullanılabilir. Alışılagelen bir kurala göre eğer n en aşağı 20 ise ve ``p`` 0,05e eşit veya daha küçük ise, Poisson dağılımı binom dağılımının bir iyi bir yaklaşımı olacaktır. Bu kurala göre eğer ``n`` a‰¥ 100 ve ``np`` a‰¤ 10 ise bu yaklaşım mükellem olacaktır.NIST/SEMATECH, ` 6.3.3.1. Counts Control Charts`, ``e-Handbook of Statistical Methods``, accessed 25 October 2006
Yeter derecede yüksek λ değeri (diyelim λ>1000) için, ortalaması λ ve varyansı λ olan bir normal dağılım, Poisson dağılım için çok iyi bir yaklaşım olacaktır. Eğer λ 10dan biraz büyük ise, bu halde normal dağılım ancak uygun bir süreklilik doğrulaması kullanılırsa uygun bir yaklaşım olabilecektir. Başka bir deyim ile, eğer P(``X`` a‰¤ ``x``) ifadeleri P(``X`` a‰¤ ``x`` + 0.5) ile değiştirilirse

F_\mathrm(x;\lambda) \approx F_\mathrm(x;\mu=\lambda,\sigma^2=\lambda)\,

olur.

Eğer bir sabit zaman aralığı içinde bir hizmet alanına gelenler sayısı, ortalaması $\lambda$ olan bir Poisson dağılımına uygun ise, o halde gelişler-arası zaman aralıkları,

oran parametresi

1/\lambda

olan, bir üstel dağılım gösterir.

Parametre tahmini

Maksimum olabilirlik

``k``_``i`` icin ``n`` tane olculmus degere kapsiyan bir orneklem alinsin. Bu orneklemin kokenindeki Poisson dagilim gosteren anakutle icin Possion parametresi olan ``λ`` icni bir uygun bir kestirim degeri bulunmasi hesaplama hedefidir.

Bu kestrimi maksimum degisebilirlik yontemi ile bulmak icin once bir bir log-degisebilirlilik fonksiyonu soyle bicimlendirilir:

L(\lambda) = \ln \prod_^n f(k_i \mid \lambda) \!

= \sum_^n \ln\!\left(\frac\lambda^\right) \!

= -n\lambda + \left(\sum_^n k_i\right) \ln(\lambda) - \sum_^n \ln(k_i!). \!

``λ`` ile ``L`` fonksiyonunun turev alinip bu turev sifira esitlenirse

\frac\lambda} L(\lambda) = 0

\iff -n + \left(\sum_^n k_i\right) \frac = 0 \!

``λ`` icin cozum yapilirsa ``λ`` icin maksimum-olabilirlilik kestirimini soyle buluruz:

\widehat_\mathrm=\frac\sum_^n k_i. \!

Her gozlem icin ortalam λ oldugu icin bu ifadenin beklenen degeri de λ olur. Bu nedenle bu kestirim λ icin bir yansiz kestirim olur. Bunun kestirim varyansi Cramer-Rao alt sinirini ulasip gectigi icin, bu kestirim bir etkin kestirimde olur.

Bayes tipi sonuç çıkartıcı analiz

Bayes tipi sonuç çıkartıcı analiz için Poisson dağılımının oran parametresi olan ``λ`` için eşlenik öncel bir gamma dağılımı gösterir. Şu ifadeye göre

\lambda \sim \mathrm(\alpha, \beta) \!

``λ``nin bir Gamma olasılık yoğunluk fonksiyonuna göre dağılım gösterdiğini; ``g``nin bir şekil parametresi olan ``α`` ile bir ters ölçek parametresi olan ``β`` ile parametrelenmiş oldugunu, şöyle güsterilsin

g(\lambda \mid \alpha,\beta) = \frac \; \lambda^ \; e^ \qquad \mbox\ \lambda>0 \,\!.

O zaman, daha önce olduğu gibi ``n`` sayıda ölçülmüş değerden oluşan örneklem ``k``_``i`` ve bir Gamma(``Î±``, ``Î²``) dağılımlı öncel verilmiş ise, sonrasal dağılım şu olur:

\lambda \sim \mathrm(\alpha + \sum_^n k_i, \frac + n}). \!

Sonrasal ortalama olan E[3] limitte

\alpha\to 0,\ \beta\to 0

doğru gittikçe maksimum olabilirlik kestirimi olan

\widehat_\mathrm

ifadesine yaklaşır.

Eklecek verilerin sonrasal tahmin edici dağılımı bir Gamma-Poisson dağılım yani bir negatif binom dağılımı olur.

Küçük sayılar kuralı

``Kural`` sözcüğü istatistik bilimi içinde ``olasılık dağılımı`` kavramı ile eşanlamlı olarak kullanılmaktadır. ``Kurala göre yakınsama`` kavramı ``dağılımda yakınsama`` ile aynı anlamda kullanılmaktadır. Buna dayanarak ``Poisson dağılımı`` bazan ``küçük sayılar kuralı`` olarak anılmaktadır. Buna neden bu dağılımın, nadir olacağı kabul edilmekle beraber, bir çok fırsatta ortaya çıkanbilen bir olayın ortaya çıkma sayısını açıklayan olasılık dağılımı olmasıdır. 1898de Ladisladus Bortkiewicz`in Poisson dağılımı hakkında yayınladığı kitabın adı ``Küçük Sayılar Kuralı``dır. Bazı matematik tarihçileri buna izafeten Poisson dağılımının adının da Bortkiewicz dağılımı olmasını istemişlerdir.[4]

İçsel Kaynaklar

Bileşik Poisson dağılımı

Tweedie dağılımı

Poisson sureci

Poisson regresyonu

Poisson örneklemesi

Kuyruk kuramı

Erlang dağılımı ``n`` sayıda olayın tümüyle ortaya çıkmasına kadar bekleme zamanlarını tanımlar. Zaman içinde dağılım gösteren olaylar için Poisson dağılımı, daha önceden aralığı sabit olarak tayin edilmiç zaman birimi içinde ortaya çıkan olay sayısını verir; Erlang dağılımı ise ``n``inci olayın olup bitmesine kadar geçen zamanının olasılık dağılımını inceler.

Skellam dağılımı: Mutlaka ayni asıl dağılımdan ortaya çıkmayan iki Poisson değişirin farkının dağılımını verir.

Tamamlanmamış gamma fonksiyonu: Yığmalı olasılık fonksiyonunun hesaplanması için kullanılır.

Dobinski`nin formülü ( dağılımı için [moment]lerin kombinatrik hesapla yorumlanması)

Schwarz formülü

Robbins ön kuramı: Empirik Bayes yönteminin Poisson dağılıma bağlı olduğunu gösteren bir ön kuram

Kaynak

Kaynak wiki

|url=http://en.wikipedia.org/w/index.php?title=Poisson_distribution|tarih= Mart 2008 |dil=İngilizce|madde=Poisson_distribution

Linkler

Online Vizülizasyon Aletleri

Referans kitapları ve makaleler

cite book

| author = Donald E. Knuth

| title = Seminumerical Algorithms

| publisher = Addison Wesley

| series = The Art of Computer Programming, Volume 2

| year = 1969

cite journal

| author=Joachim H. Ahrens, Ulrich Dieter

| title=Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions

| journal=Computing

| year=1974

| volume=12

| issue=3

| pages=223--246

| doi=10.1007/BF02293108

cite journal

| author=Joachim H. Ahrens, Ulrich Dieter

| title=Computer Generation of Poisson Deviates

| journal=ACM Transactions on Mathematical Software

| year=1982

| volume=8

| issue=2

| pages=163--179

| doi=10.1145/355993.355997

cite journal

| author=Ronald J. Evans, J. Boersma, N. M. Blachman, A. A. Jagers

| title=The Entropy of a Poisson Distribution: Problem 87-6

| journal=SIAM Review

| year=1988

| volume=30

| issue=2

| pages=314--317

İnternet Siteleri

Olasılık Dağılımları|Poisson dağılımı İstatistik

Kaynaklar

Vikipedi

Poisson Dağılımı

Örnekler

Tarihçe

Nadir olaylar için Poisson dağılımı

Özellikler

Poisson dağılımı ile üretilen rassal değişkenlerin simulasyonu

İlişkili dağılımlar

Parametre tahmini

Maksimum olabilirlik

Bayes tipi sonuç çıkartıcı analiz

Küçük sayılar kuralı

İçsel Kaynaklar

Kaynak

Linkler

Online Vizülizasyon Aletleri

Referans kitapları ve makaleler

İnternet Siteleri

Kaynaklar

İlgili konular

Negatif binom dağılımı

Skellam dağılımı

Olasılık dağılımı

Binom dağılımı

Faktöriyel moment

Poisson denklemi

İstatistiksel terimler, kavramlar ve konular listesi

Normal Dağılım

Poisson Dağılımı

Poisson Dağılımı Hakkında Detaylı Bilgi

Örnekler

Tarihçe

Nadir olaylar için Poisson dağılımı

Özellikler

Poisson dağılımı ile üretilen rassal değişkenlerin simulasyonu

İlişkili dağılımlar

Parametre tahmini

Maksimum olabilirlik

Bayes tipi sonuç çıkartıcı analiz

Küçük sayılar kuralı

İçsel Kaynaklar

Kaynak

Linkler

Online Vizülizasyon Aletleri

Referans kitapları ve makaleler

İnternet Siteleri

Kaynaklar

İlgili konular

Görüşler ve Yorumlar

Okuma Önerileri

Negatif binom dağılımı

Skellam dağılımı

Olasılık dağılımı

Binom dağılımı

Faktöriyel moment

Poisson denklemi

İstatistiksel terimler, kavramlar ve konular listesi

Normal Dağılım