Viskozite

 Gazlar gibi  sıvılarda akmaya karşı bir direnç gösterirler. Akışkanların gösterdiği bu  dirence viskozluk denir ve genellikle η ile simgelenir. Viskozluğun tersi olan  niceliğe akıcılık denir ve genellikle ф ile simgelenir. Akıcılık ve viskozluk ф  = 1/ η eşitliğine göre ters orantılıdır. Viskozitesi yüksek olan sıvının  akışkanlığı düşüktür. Örneğin viskozluğu daha yüksek olduğundan gliserin suya  göre daha yavaş akar. Sıvıların viskozluğu molekül yapıları ve moleküller arası  etkileşmelerle yakından ilgilidir.

 Herhangi bir  boru içinde akan bir sıvının akış hızı akımı sağlayan yürütücü kuvvet ile akımı  engellemeye çalışan direncin büyüklüğüne bağlıdır. Akımın yürütücü kuvveti  borunun iki ucu arasındaki basınç farkından, engelleyici kuvvet ise sıvı  moleküllerinin birbiri ile ve aktıkları borunun çeperleri ile yaptıkları  sürtünmelerden doğmaktadır. İngiliz mühendis Osborne Reynolds (1842-1912) 1883  yılında akım hızına bağlı olarak farklı iki akımın varlığını denel yoldan  göstermiştir. Buna göre, düşük hızlarda sıvı moleküllerinin akım yönünde olmak  üzere bir boyutlu, yüksek hızlarda ise üç boyutlu öteleme hareketi yaptıkları  ortaya çıkmıştır. Düşük hızla akan bir sıvıda her molekül bulunduğu düzlemi  akış süresince hiç değiştirmemekte ve sanki sıvı moleküllerinden oluşan  düzlemler şekil A da görüldüğü gibi birbiri üzerinden farklı hızlarda akış  yönüne doğru kaymaktadırlar. Bu tür akımlara laminer akım, tabakalı akım veya  viskoz akım denir. Moleküllerin, akım yönünde daha hızlı olmak üzere her yöne  doğru hareket ettiği yüksek hızdaki sıvı akışına türbülent akım veya kargaşalı  akım denir.

 Akış hızı  yükseltilerek belli bir hızda laminer akımdan türbülent akıma geçilir. Bu geçiş  hızına kritik hız denir. Viskozite, yoğunluk ve akış borusunun iç çapına bağlı  olan kritik hız, her sıvı için ve her boru için farklıdır. Akımın türünü,  sıvının yoğunluk ve viskozluğu ile borunun çapından bağımsız olarak belirlemek  üzere boyutsuz bir nicelik olan ve

 Şeklinde tanımlanan Reynolds sayısı  kullanılır. Burada; D borunun iç çapını, u akış hızını, ρ yoğunluğu, η ise  viskozluğu simgelemektedir. Eğer Reynolds sayısı 2100 ile 4000 arasında iken  kararsız bir durum vardır ve bu aralıkta laminer akımdan türbülent akıma  dönüşme olur.

 Sürtünmeden  dolayı boru çeperlerinde sıfır olan sıvının akış hızı boru çeperlerinden  merkeze doğru yükselir. Sıvı hızı u ve çeperden uzaklık z ile simgelendiğinde  akış hızındaki bu yükselme Şekil A ve B de görülmektedir. Şekil B deki u=f(z)  eğrisinin herhangi bir noktadaki eğimi (du/dz) hız gradyenti olarak tanımlanır.  Akış hızının çeperden uzaklıkla değişme hızı olan hız gradyenti boru çeperinde  maksimum, boru merkezinde ise sıfırdır. Hız gradyentinin çeperden olan z  uzaklığı ile değişimi Şekil C de görülmektedir. Buna göre laminer akım için  düşündüğümüz sıvı tabakalarının hızları çeperden boru merkezine doğru  gidildikçe yükselmektedir.

Sürtünme basıncı, sürtünme kuvveti ve viskozluk;

   Birbirine  değerek farklı hızlarda akan sıvı tabakalarından birbirinin birim alanına etkiyen  kuvvete sürtünme basıncı denir. Sürtünme kuvveti F, sürtünen yüzeyin alanı A  ile gösterildiğinde τ ile simgelenen sürtünme basıncı

 τ =F/A

şeklide verilir.sürtünme basıncı hız gradyenti ile doğrusal olarak değişen akışkanlara “Newtonyen akışkanlar” denir. Newtonyen akışkanlar Şekil D deki N doğrusu ile temsil edilmektedir. Gazlar, çözeltiler ve koloidal olmayan sıvılar Newtonyen akışkanlardır. Newtonyen akışkanlar için N doğrusundan, η orantı katsayısı olmak üzere sürtünme kuvveti için

τ~du/dz, τ=η(du/dz), F/A= η(du/dz), F= ηA(du/dz)

eşitliği bulunur. Buradaki η orantı katsayısı akışkan için mutlak viskozluk olarak alınır. Viskozluğun SI deki birimi son bağıntıdan Nsm-2=kgs-1.m-1 olarak bulunur. CGS deki viskozluk birimi ise yine son bağıntıdan dynscm-2=gs-1cm-1=P olarak bulunur ve poise olarak adlandırılarak p ile simgelenir.

   Şekil D deki  x,y ve z eğrileri Newtonyen olmayan akışkanlara aittir. Bingham akışkanları x  doğrusuna uymaktadırlar. Bu sıvılar, sürtünme basıncı belli bir τ0  değerini aşmadıkça akmazlar. Ancak bu değerden sonra sürtünme basınçları hız  gradyenti ile doğrusal olarak değişir. Kil süspansiyonları ve bazı plastikler  bu türdendir. Lastik kauçuğu gibi sahte plastiklerin akışı y eğrisi ile  karakterize edilir. Bazı emülsiyonlar için geçerli olan ve z ile karakterize  edilen akışkanlara dilatant akışkanlar adı verilir. Newtonyen olmayan  akışkanların akışı reoloji konuları arasına girmektedir.

   Poiseuille  denklemi;

   Şekil A da  görülen yarıçapı z ve uzunluğu l olan bir sıvı silindirin akabilmesi için bu  silindir üzerine etkiyen basınç kuvvetinin en az sürtünme kuvvetine eşit yada  ondan büyük olması gerekmektedir. Buna göre kuvvet denkliğinden

   F(basınç  kuvveti)=F(sürtünme kuvveti)

(ρ1- ρ2)πz2=η(2πzl)x(du/dz)

eşitliği bulunur. Akış hızı u olduğundan bir saniyede akan sıvının hacmi yarıçapı z ve uzunluğu u olan silindirin v=πz2u hacmine eşittir. Buradan, akan hacmin hızla değişimi için dv/du= πz2 yazılır ve son eşitlik ile birleştirilirse

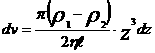
   eşitliği bulunur. Buna göre r yarıçaplı  borudan birim zamanda akan sıvının tüm hacmi yani v hacimsel debisi

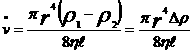
eşitliği ile bulunur. İlk kez Fransız hekim ve fizikçi Jean Lois Poiseuille (1799-1869) tarafından üretildiği için bu eşitliğe Poiseuille denklemi denir.

   Eğer akışkan  bastırılabilen yani gaz yada buhar ise   hacimsel debisi ρ1  ve ρ2 basınçlarında farklıdır. Giriş ve çıkış basınçlarının aritmetik  ortalaması için hacimsel debi hesaplanmak istenirse ρ0 standart basınç  olmak üzere Boyle-Mariotte yasasından

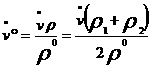
yazılabilir. Son iki bağıntının birleştirilmesiyle gaz ve buharların viskozitesi için Hagen-Poiseuille denklemi

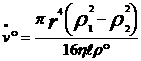
şeklinde yazılabilir.

   Absise du/dz  hız gradiyenti, ordinata sürtünme stresi τ, koyularak çizilen grafiklerde, saf  sıvıların büyük kısmı ve bazı çözeltiler bir doğru verir, bu sıvılara  “Newtonyen” sıvılar denilir. Ancak, endüstride kullanılan koloidal emülsiyonlar  ise bir doğru vermezler, Dilatant, Pseudoplastik ve bingham gibi değişen farklı  akış özellikleri gösterirler. Dilatant emülsiyonlarda, du/dz hız artışı ile τ,  sürtünme stresi Newtonyen çözeltilerden daha fazla arttığından, yukarı dönen  bir eğri, Pseudoplastik emülsiyonlarda tersine aşağı dönen bir eğri gösterir.  Bingham emülsiyonlarda ise ancak belli bir sürtünme stresinden sonra sıvıda  akmaya başlar. 

 
Τ0

 
Newtonyen

 
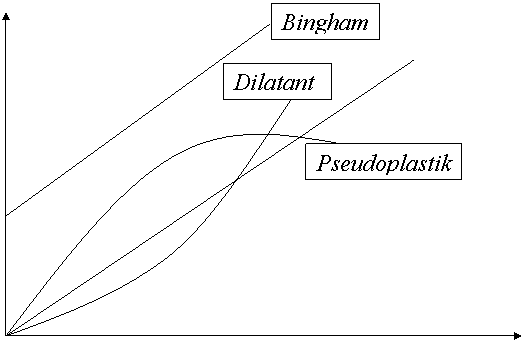
Sürtünme hızı

Viskozitenin sıcaklıkla değişimi: bir akışkanın viskozitesi ile sıcaklığı arasında

   ilişki vardır ve iki tarafın  logaritmasını alırsak,

   bulunur. Burada A bir sabit Ea  ise aktivasyon enerjisidir.

   Koloidal  emülsiyonların viskozitenin seyrelme ile değişimi: koloidal emülsiyoblarda, su  içinde çözünmeyen mikron büyüklüğünde kürecikler halinde koloidal tanecikler  vardır. Bunlar emülsiyon polimerizasyonla elde edilen sentetik polimerler yada  gıda sanayinde doğal makromoleküller, veya yağlar halinde olabilir. Bunların  akmaya karşı dirençleri birbirleri üzerinden kayabilme yeteneklerine, bu da  seyreltik veya konsantre olmalarına, yani çözeltideki konsantrasyonlarına  bağlıdır. Yalnız bu durumda az miktarda bir seyrelmenin bile vizkozite üzerinde  büyük etkisi vardır. Endüstride koloidal emülsiyonlar da konsantrasyon birimi  olarak genellikle katı madde miktarı kullanılır. Katı madde azalmasıyla  viskozite azalması arasında basit bir ilişki yoktur, koloidin ve ortamın  cinsine göre değişir. 

DENEYİN YAPILIŞI: Dönel viskozimetre ölçüm öncesinde tam dik olarak yerleştirilmelidir, bunun için kontrol hava kabarcığının cihazın solundaki dairenin ortasında olup olmadığı kontrol edilir, değilse ayak vidaları ayarlanarak düzeltilir. Viskozitesi ölçülecek yağın ısıtıcı üzerindeki behere konulur, beher içine karıştırıcı balığı atılır. Behere termometre sokularak sıcaklık ölçülür. Seçilen metal silindir viskozimetreye takılır, üzerine koruma demiri takılır, sonra beher içindeki sıvı içine silindirin ince borusu üzerinde işaretli yere kadar daldırılır. Kullanılacak dönme hızı seçilir, ve soldaki düğme ile bu hız ayarlanır. Arkadaki kontrol çubuğuna basılır ve bundan sonra cihazın başlama düğmesi çalıştırılır. Gösterge skalası dönmeye başlar ve 10 saniye sonra kontrol çubuğu bırakılır ve kırmızı gösterge yer değiştirerek 20-30 sn sonra bir noktada sabitlenir ve tekrar arkadaki kontrol çubuğuna yavaşça basılır, kırmızı gösterge artık yerini değiştiremez, kontrol çubuğuna basılı iken motor durdurulur ve o dönme hızı ve silindir numarası için % kaç torsiyon direnci olduğu göstergeden okunur bundan sonra arkadaki kontrol çubuğu bırakılarak sistem ilk haline dönmüş olur. Okunan % değer cihazın üzerindeki tabloda verilen katsayı ile çarpılarak akışkanın viskozitesi mPa-s cinsinden okunur. Okunan değerin % 30-80 arasında olması beklenir, daha az veya fazla ise dönme hızını tekrar ayarlamak gerekir. Daha sonra beher altındaki ısıtıcı ve karıştırma açılır, beher sıcaklığının 10˚C yükselmesi beklenir. Sonra sadece ısıtıcı kapatılır, 10 dakika beklenerek termal dengeye gelinir, karıştırıcı bu arada çalıştırılır. Karıştırıcı da kapatılır, termometre ile son sıcaklık ölçülür ve viskozimetre çalıştırılarak viskozite ölçümü yapılır. Benzer şekilde 4 değer daha alınır ve oda sıcaklığı ile bundan 50˚C yüksek sıcaklık arasında 5-6 nokta alınarak viskozite sıcaklık ilişkisi incelenir.

GEREKLİ ALET VE MALZEMELER: Dönel viskozimetre, ısıtıcı, ince uzun cam beher, tuvalet kağıdı, yağlar.

HESAPLAMALAR:

1 nolu rotor; T=24.1˚C

   6 rpm → 31.5 x 10 = 315 mPa.s

   *12  rpm → 62 x 5 = 310 mPa.s

   30 rpm → 100<<

   60 rpm → 100<<

2 nolu rotor; T=24.1 ˚C

   6 rpm → 6.5 x 50 = 325 mPa.s

   12 rpm → 12.5 x 25 = 312.5 mPa.s

   30 rpm → 31 x 10 = 310 mPa.s

   60 rpm → 62 x 5 = 310 mpa.s

En uygun 1 nolu rotor 310 mPa.s

1 nolu rotor; T=32.6˚C

   6 rpm → 17 x 10 = 170 mPa.s

   *12  rpm → 34.5 x 5 = 172.5 mPa.s

   30 rpm → 84.5 x 2 = 169 mPa.s

   60 rpm → 100<<

1 nolu rotor; T=40˚C

   6 rpm → 11 x 10 = 110 mPa.s

   12 rpm → 21.5 x 5 = 107.5 mPa.s

   *30  rpm → 53.5 x 2 = 107 mPa.s

   60 rpm → 100<<

η(mPa.s)     T˚C       T˚(K)         1/T            η(Pa.s)           lnη

   310             21.4       294.55    3.395x10-3    310x10-3         -  1.1712

   172.5        32.6         305.75     3.271x10-3    172.5x10-3   -  1.7574 107           40            313.15    3.193x10-3     107x10-3       - 2.2349

Grafikten bulduğumuz denklem;    y=5327,87x - 19,23

   düzenlersek;

    lnη=5327,87 - 19,23

   lnη=-lnA

   m=5327,87=   Ea= 44295,91 J/mol

    n=-19,23=-lnA  A= 2,246x108 Pa.s

SONUÇLAR:

   Grafik  denklemi:    y=5327,87x - 19,23

    m=5327.87, n=-19,23

   Ea=44295  J/mol

   A=2,246x108Pa.s 

YORUM: Yaptığımız deneyde viskozitenin sıcaklıkla değişimini inceledik. Bu deneyde yapmış olduğumuz hata rotorların  her kullanımda iyi temizlenmemiş olmasından kaynaklanıyor olabilir. Yada skalayı doğru okuyamadığımızdan  kaynaklanmış olabilir.

KAYNAKLAR: Fizikokimya laboratuar föyü

                             Fizikokimya →Prof.  Dr. Yüksel SARIKAYA