Sonuşmaz
Kısaca: Matematikte sonuşmaz veya asimptot (İngilizcesi: ''Asymptote''), belirli bir ''A'' eğrisine istenildiği kadar yaklaşabilen ikinci bir ''B'' eğrisine verilen addır. Bir başka deyişle, ''A'' üzerinde ilerledikçe, ''A'' ve ''B'' arasındaki mesafe azalır ve sıfıra yaklaşır. ''Asimptot'' kelimesi, Yunanca "beraber düşmek" anlamındaki ''simpiptein'' fiilinin olumsuz halinden türemiştir. ...devamı ☟
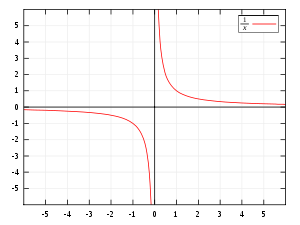
Sonuşmaz
Türkçe Sonuşmaz kelimesinin İngilizce karşılığı.n. asymptote