Türkçe Bilgi: Pisagor

Pisagor (Pythagoras), Yaklaşık olarak MÖ 580 - MÖ 500 tarihleri arasında yaşamış olan Yunan filozofu.

Doğum yeri olan Sisam adasından M.Ö. 529'da Güney İtalya'ya, Crotona'ya göç etti. Crotona bu yörenin zengin liman kentlerinden biriydi. Pisagor burada biraz kişisel çekiciliği, kendinde varolduğunu iddia ettiği kehanet gücü, biraz da etrafında yarattığı gizemci havasıyla zengin ve soylu delikanlılardan üçyüz kadarını bir çatı altında topladı ve okul kurdu. Pisagor öğrencilerini iki bölüme ayırıyordu : Dinleyiciler ve matematikçiler. Okula dinleyicilik ile başlanıyor başarılı olunursa matematikçiliğe geçiliyordu.

Antik Çağ'ın en ünlü adlarından biri olan Pythagoras (Pisagor) çok yönlü kişiliği yanında matematikçi sıfatım layıkıyla haketmiştir. Bu Eski Yunan filozofu ve bilim adamının günümüzde dahi geçerli ve tüm zamanlar için de geçerliliğim koruya • cağı anlaşılan ünlü teoremi, bu savı doğrulamak için yeterli bir nedendir. "Düzlemde, bir dik üçgende, dik kenarlar üzerine kurulan karelerin a-lanları toplamı, hipotenüs üstüne kurulan karenin alanına eşittir."

"Pisagor Teoremi" olarak tanınan bu teoremin, Pisagordan önce Çin'li Çu Pei tarafından bilindiği ve kanıtlandığı, Sümerler ve Babiller gibi eski uygarlıklarda kenarları 3,4,5 birim olan üçgenlerin "dik üçgen" olduğunun bilindiğine dair bilgiler mevcutsa da, Pisagor'un farkı, bu teoremi bir matematikçi yaklaşımıyla ve genelleyerek vermiş olmasındadır.

İyi yetişmiş ve gençliğinde iyi bir eğitim almış olan Pisagor, çok ve sıkça seyahatler yapmıştır. Babil ve Mısır'da geçirdiği uzun yıllar O' nun bilimine önemli katkılarda bulunmuştur. Özellikle din adamlarından ve rahiplerden çok yararlandığı bilinmektedir. Bu sırada dini eğitim de almıştır.

Bir süre Çin'e de gitmiş ve bir kaç yılını da orada geçirmiştir.

53 yaşında ülkesine, Sisam adasına geri dönmüştür. Sisam adası bilindiği gibi ülkemize en yakın Ege adalarından biridir nın karşında. Demek ki Pisagor da bir Egelidir. Edindiği deneyimleri, artık olgun ve yetkin bir insan olarak bir okul kurmak suretiyle, başkalarıyla paylaşmak istemektedir. Tarihte "Pisagor Okulu" olarak bi-

linen ve tanınan bu okulun kendine özgü konuları ve eğitim biçimi vardı. O kendi anlayışına göre bir eğitim sistemi geliştirmiş bulunuyordu. O'nun mistik anlayışı "sayılar" ile birleşince, evreni sayılarla temsil etmek düşüncesi, sonuçta Pisagor-culuk denilen bir anlayışı ortaya çıkarmıştır. Matematik ile ilgili uğraşısı çok yönlüdür. Ünlü teoremi dışında, özel likle sayılara ilişkin çalışmaları, o zamanlar için çok ileri düzeyde sayılabilir. Bazı özel sayı kavramları O'nun zamanında ortaya atılmıştır. Örneğin dost sayılar, heteromek sayılar ; üçgensel, tam-kare sayılar gibi örnekler çoğaltılabilecektir.

Tam bölenlerinin toplamı birbirini veren sayılara dost sayılar denir. Örneğin 284 ve 220 sayılan gibi... n(n+l) gibi sayı gruplarına heteromek sayılar, V2 n(n+l) gibi sayılara üçgensel sayılar, n2 ile temsil edilenlere ise tam kare sayılar denilmektedir.

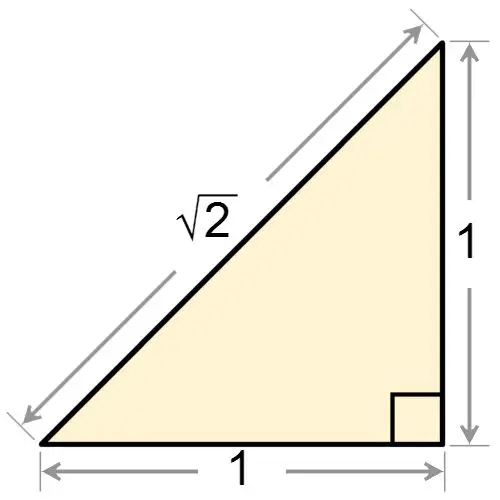
O'nun bir de sayı mistisizmi vardır ki, O'na göre "doğada her şeyin karşılığı bir sayı"dır. Bu mistik anlayışı temsil etmektedir. Ancak 2 ve 5 sayılarının onların nezdinde çok ayrıcalıklı bir yeri vardı. Çünkü bunlar mukaddes sayılardır. 7 ve 10 sayılarının da diğerlerinden farklı olan bir ayrıcalığı bulunmaktadır. Bu tür yaklaşımlar, insanların ya da bilginlerin sayılara yaklaşımını ve bakış açısını değiştirmiş ve bir çok araştırmanın yapılmasına olanak sağlanmıştır. Pisagor Okulu'nun temel felsefesinde 1,2,3,...gibi giden tam sayılarla, bütün bir evrenin matematik, fizik, metafizik, ahlak ve her-şeyin, "süreksiz" bir modelini kurabileceği düşüncesi vardır. Bunlann, tanrının işi olduğuna inanıyorlardı. Bazen yenilgileri de oluyordu. Örneğin dik kenarları a ve b ve hipotenüsü c ile gösterilen bir dik üçgende Pisagor teoremi ile temsil edildiğine göre, a=l,b=l olan bir dik üçgende c2 = 2 olması ve bundan c = y2 çıkması akıllannı kanştırıyordu. Bir yenilgileri de sayıları düzenledikleri zaman ortaya çıkacaktır. 0 % lA 3/4 1 Tam sayılan tanıyorlardı ve onları bu şekilde görüldüğü gibi bir sayı doğrusu üzerine dizmeyi düşünmüşlerdi. Bütün rasyonel sayıları (örneğimizde 0 ile 1 arasındaki) sayıları sıraladıktan sonra, sayılarla doğrunun noktalan arasındaki birebir eş-leşme konusundaki bulgulan onları şaşırtıyor ve doğrunun üzerinde henüz karşılığına sayı konulmamış noktaların bulunduğunu anlıyorlardı.

Antik çağ' da henüz İrrasyonel Sayılar tanınmadığı için, buna yanıt bulmakta güçlük çekiyorlardı. Aradan yüzyıllar geçecek ve Reel Sayılar tanımlandıktan sonra ancak bunun yanıtı verilebilecektir. Pisagor Okulu geometri 'ye de ilgi duymuş, sentetik anlamda da olsa bazı önemli buluşlara adlanm yazdırmışlardır. Örneğin (a+b)2 (a + b)2 = a2 + 2ab + b2

ab a2 b2 ab ilişkisini şekilde görüldüğü gibi, geo -metrik olarak açıklayabiliyorlardı. Onlann yine sayılara dönük çalışmaları arasında bir başka yenilgileri varlığına inandıklan bazı sayıları bu -kınayacaklarının anlaşılmasıdır.

Onlar, " biri diğerinin iki katımı e-şit olan tamkare sayılar" arıyorlardı. Eğer bu sayılar a ve b ise bu iddiaya göre, a = 2b2 eşitliğini sağlamalan gerekirdi. Bu olanaksızdır. Bu olanaksızlık kanıtlanmıştır/1* Bu da Pisagor okulunun yenilgileri arasında yer almıştır.

Pisagor okulu zamanla bir bilim ve felsefe okulu olmaktan çıkmış dini eğitimi esas alan bir okula dönüşnüşmüştür. Antik çağ henüz din konusunu aşmış değildir. Tek tanrıcılar ile çok tanrıcılar devamlı bir çatışma halindedirler. Pisagor da işte bu çekişmenin kurbanlarından biri olacaktır. Bunun başka örneklerine ileride yine rastlanacaktır. Öğrencileriyle ders yaptığı bir akşam, okul karşıt dincilerce basılacak ve ateşe verilecektir. İçindekiler öldürülecek, Pisagor ise okulundaki yangını söndürmek için oradan oraya koşuştururken alevler arasında kalarak can verecektir. (D Bu kanıt için bkz : Y.AKSOY, Matematik [1] Tarihi Cilt 1, syf. 125 / YTÜ Yayını, Sayı 474,1999

Pisagor

İlgili konular

Pisagor Resimleri

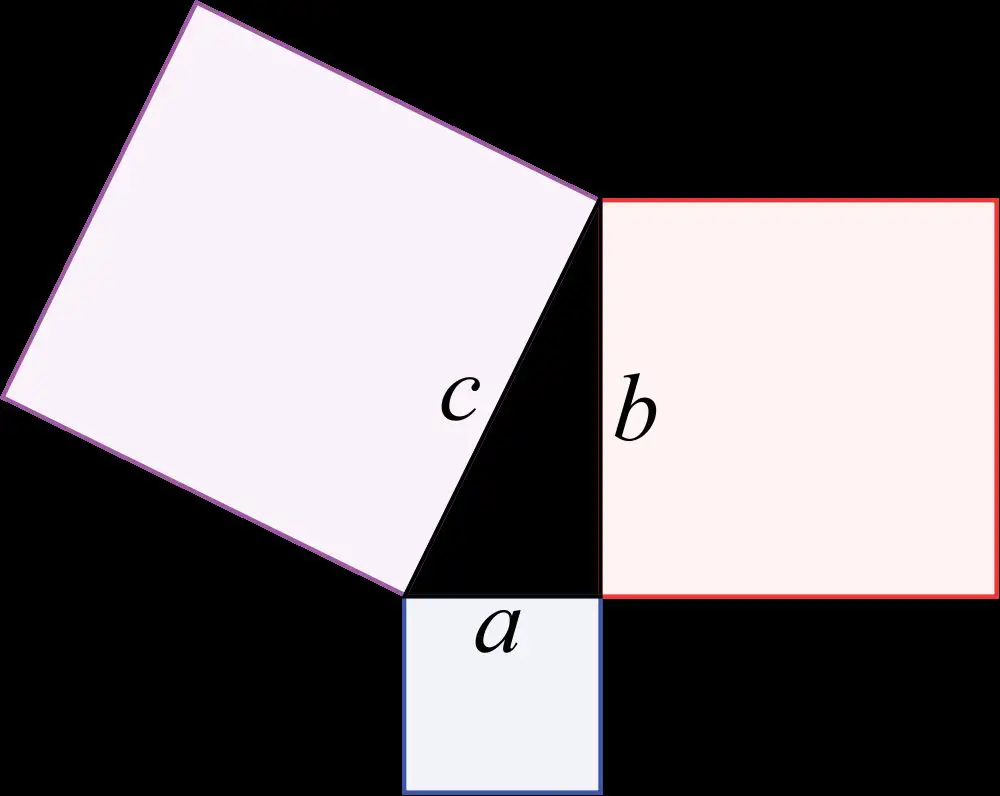
Pisagor teoremi

Pisagor üçlüsü

Pisagor inisiyasyonu

Pisagor toplamı

Diyofantus denklemi

Yunan matematiği

Pisagorculuk

Hippasus