Konikler
Kısaca: Konikler Eliptik veya dairesel bir çift taraflı koninin, düzlemle kesitinden meydana gelen eğriler. Bunlar, elips, parabol ve hiperboldür. Elips: Aralarındaki mesafe 2a olan ve odak noktaları denen iki noktaya uzaklıkları toplamı, sabit 2a’ya eşit olan noktaların geometrik yeridir. Elips oval bir eğri olup, iki dik simetri ekseni mevcuttur. Bunlar, bir M noktasında kesişirler. Bu eksenler koordinat takımı olarak alınırsa, elipsin denklemi; b2 = a2 - c2 olmak üzere x2/a2 + y2/b2 = 1 şek ...devamı ☟
Elips: Aralarındaki mesafe 2a olan ve odak noktaları denen iki noktaya uzaklıkları toplamı, sabit 2a’ya eşit olan noktaların geometrik yeridir. Elips oval bir eğri olup, iki dik simetri ekseni mevcuttur. Bunlar, bir M noktasında kesişirler. Bu eksenler koordinat takımı olarak alınırsa, elipsin denklemi; b2 = a2 - c2 olmak üzere x2/a2 + y2/b2 = 1 şeklinde belirir. Eğer c= 0 olursa, odaklar birbiriyle çakışır ve elips yarıçapı a=b eşit olan bir çembere dönüşür. (Bkz. Elips)
Hiperbol: Hiperbol, belirli iki noktaya olan mesafelerinin farkı, sabit 2a’ya eşit olan noktaların geometrik yeridir. Bu sabit noktalar, hiperbolün odak noktaları olarak isimlendirilir ve ara mesafesi 2c olarak gösterilir. Hiperbolün iki ayrı kolu mevcut olup, birbirine dik iki simetri ekseni mevcuttur. Bu eksenlere göre hiperbolün denklemi, b2 = c2 - a2 olmak üzere x2 / a2 - y2 / b2 = 1 olarak yazılır. y=± bx/a doğruları hiperbolün asimptotlarıdır.
Parabol: Parabol, belirli bir noktaya ve bir doğruya uzaklıkları eşit olan noktaların geometrik yeridir. Bu belirli noktaya parabolün odak noktası denir. Bu noktadan doğruya çizilen dik doğru, parabolün simetri eksenini teşkil eder. Parabolün bu eksene ve tepe noktasından geçen dik eksene göre denklemi y2 = 2px olarak belirir.
Koniklerin genel denklemi: Dik x ve y koordinat ekseninde ikinci dereceden genel bir denklem;
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F= 0 olarak belirir. Eğer A,C ve F katsayılarının hepsi birden sıfır değilse bu bir konik kesitini gösterir. Ancak bu halde konik kesiti yanında birbirini kesen iki doğru veya iki paralel doğru, üst üste bulunan iki doğruyu da kapsar. Bunlar b2 x2 - a2 y2 = 0 (x+a)= 0 veya x2 = 0 olabilir. Ayrıca koniğin, x2 / a2 + y2 / b2 = -1 gibi sanal da (izafi de) olabilir ve x ve y koordinat ekseninde gösterilmez. İki konik en fazla dört noktada kesişir.
Tarihi gelişimi: İlk koni ile ilgilenen M.Ö. 350 civarında Menaechmus olmuştur. Bu konuda ilk kitap M.Ö. 320’de Euclid tarafından yazıldığı tahmin edilmektedir. Günümüze kadar gelen kitap M.Ö. 225’ten, Apollonius’un Konikler kitabıdır. Arşimet (M.Ö 287-212), konikleri tanımaktaydı ve çalışmalarında bunları kullanmıştır. Abbasi alimlerinden Beni Musa’nın konikler üzerine yazdığı Kitab-ül-Mahrutat kitabı Ünlüdur. Ebu Sa’id-el-Siczi ise koni kesitlerini incelemiştir.
Konik kelimesi, Apollonius tarafından verilmiştir. y2 = 2px+ax2 ifadesinde eğer a<0 ise hiperbol a>0 ise elips ve a=0 ise parabol ortaya çıkar.
Rönesansta, özellikle Kepler, gezegenlerin eliptik yörünge üzerindeki hareketini keşfettikten sonra, koniklere olan ilgi tekrar canlanmıştır. Descartes’in 1637’de analitik geometriyi keşfetmesinden sonra, cebirsel metodlar eski geometrik metodların yerini almıştır. Günümüzde konikler, ders kitaplarında, daha çok analitik geometrinin konusu olarak anlatılmaktadır.
Kaynak: Rehber Ansiklopedisi
Konikler Resimleri
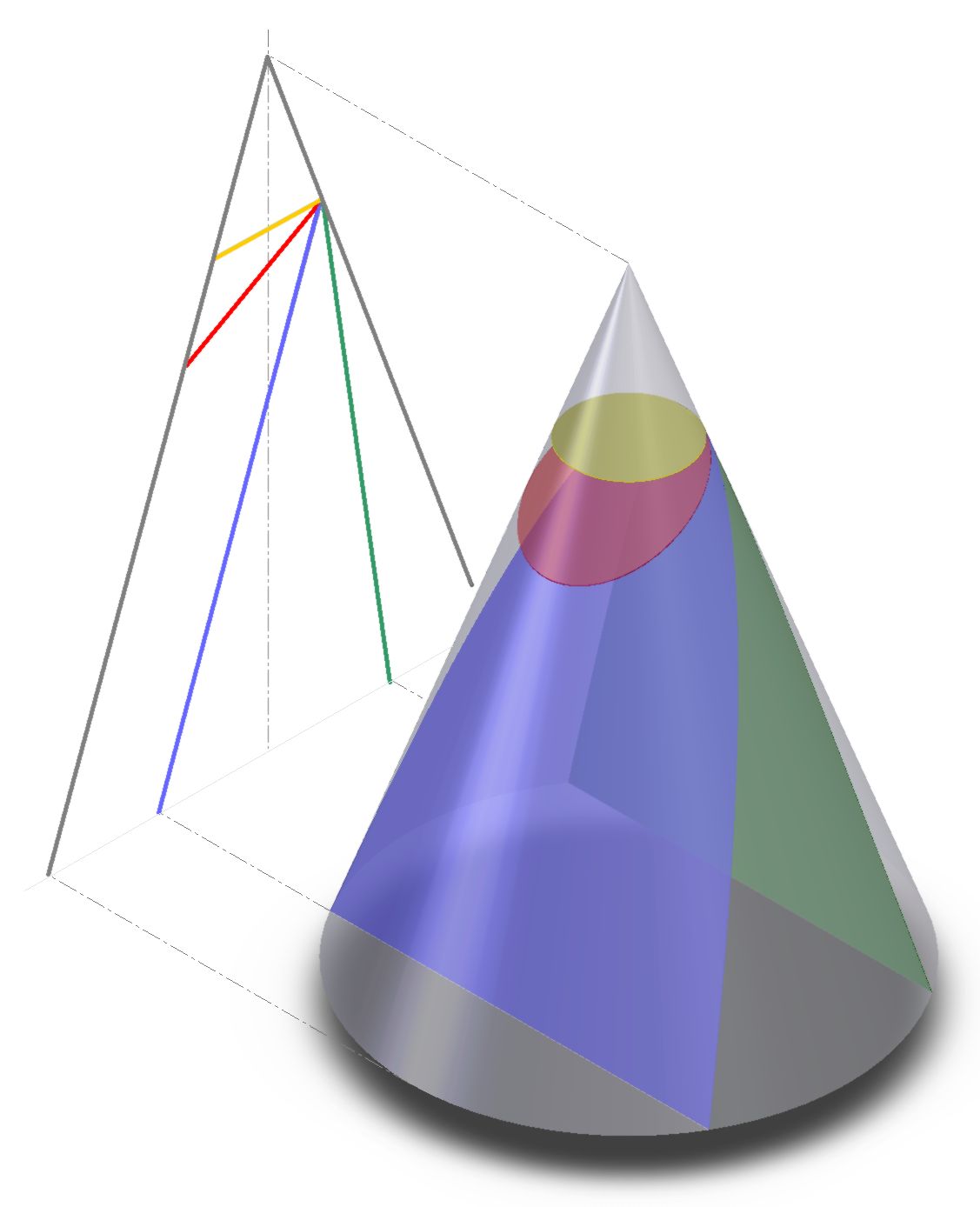
Konik
3 yıl önceGeometride, bir dönel koninin bir düzlemle arakesiti; daire, elips vb. konikler Volkan bilimde, ana bir kraterle sonlanan yanardağlar Tekstilde, İplik...
Konik, Daire, Elips, Geometri, Koni, Konikler, Krater, Volkan, Yanardağ, İplik, MasuraKONİK PROJEKSİYON
3 yıl önceKonik projeksiyon, kürenin koni şeklindeki bir kağıda sarılmasıyla oluşturulan bir harita hazırlama yöntemidir. Bu yöntemle çizilmiş haritalarda şekil...
Konik projeksiyon, Coğrafi terim, Enlem, Harita, Kağıt, Koni, TaslakHelisel konik yay
7 yıl önceHelisel konik yay, daire veya dikdörtgen kesitli bir telin bir eksen etrafında konik şekilde sarılmasıyla imal edilen ve burulmaya zorlanan, helisel yaylar...
Helisel konik yay, Bası yayları, Bilezik yay, Daire, Dikdörtgen, Disk yay, Eksen, Helisel silindirik yay, Helisel yay, Kangal yay, KonikHelisel yay
3 yıl öncesilindirik ya da konik şekilde sarılmasıyla imal edilen ve burulmaya zorlanan bir yay çeşididir. Helisel silindirik yaylar, Helisel konik yaylar ve kangal...
Helisel yay, Almanca, Bası yayları, Bilezik yay, Daire, Dikdörtgen, Disk yay, Eksen, Helisel konik yay, Helisel silindirik yay, Kangal yayÇİLEK
3 yıl önceuygundur. Ilıman bölgeler için uygundur. Meyve çürüklüğüne dayanıklıdır. Uzun konik koyu kırmızı renklidir. Meyve eti serttir, meyvenin saptan kopması zordur...
Çilek, Çilek, Alt cins, Alt familya, Alt oymak, Alt sınıf, Alt takım, Alt tür, Alt İ¢lem, Alt şube, AnsiklopediKoni
3 yıl önce{1}{3}}\cdot \pi \cdot r^{2}\cdot h} Bir dönel koninin düzlemlerle arakesitine, konikler adı verilir. Herhangi bir koni, tabana paralel bir düzlemle kesilirse,...
Koni, Geometrik, Konikler, MatematikMenaechmus
3 yıl önceChersonese'deki Prokonnesos'ta doğmuş, Platon'la olan arkadaşlığı ile tanınan, konik kesitlerini açık keşfiyle ve parabol ile hiperbol kullanarak küpü iki katına...
Blaise Pascal
3 yıl önceve düşünürdür. En bilinen temel eseri Düşünceler'dir. 16 yaşındayken konikler üzerine bir inceleme yazdı. 1642'de 19 yaşında iken vergi tahsildarı babasının...
Blaise Pascal, 1623, 1662, 19 Ağustos, 19 Haziran, Felsefe Portalı, Fransız, Kişi, Taslak, Wikimedia, Düşünceler