isim =Gamma|
tip =yoğunluk|
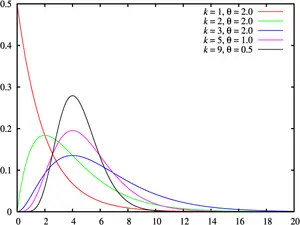
pdf_image =|
cdf_image =|
parametreler = şekil (reel)
ölçek (reel)|
destek =|
OYF =|
YDF =|
ortalama =|
medyan = basit kapalı form yok|
mod = |
varyans =|
çarpıklık =|
basıklık =|
entropi =
|
mf =|
kf =|
Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdir. Bu parametrelerden biri ölçek parametresi ``θ``; diğeri ise şekil parametresi ``k`` olarak anılır. Eğer ``k`` tamsayı ise, gamma dağılımı ``k`` tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre olur.
Karekteristikler
Bir rassal değişken olan ``X``in ``θ`` ölçek parametresi ve ``k`` şekil parametresi ile tanımlanmış bir gamma dağılımı ile ifade edilmesi için şu notasyon kullanılır:Olasılık yoğunluk fonksiyonu
Gamma dağılımının olasılık yoğunluk fonksiyonu şu şekilde bir gamma fonksiyonu ile ifade edilebilir:
\ \mathrm\ x > 0\,\, \mathrm\,\, k, \theta > 0.
Bu çesit parametrelerle ifade edilme yukarıda verilen bilgi kutusunda ve grafiklerde kullanılmıştır.
Alternatif bir şekilde, gamma dağılımının olasılık yoğunluk fonksiyonu bir şekil parametresi ile ölcek parametresinin tersi olan oran parametresi kullanılarak şöyle elde edilir:
Olasılık yoğunluk fonksiyonu her iki şekli de istatistikçiler tarafından yaygın olarak kullanılmaktadır.
Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu bir tanzim edilmiş gamma fonksiyonudur ve bir tamamlanmamış gamma fonksiyonu şeklinde şöyle ifade edilir:
=\frac \,\!
Özellikler
Toplama
Eğer ``i`` = 1, 2, ..., ``N`` için rassal değişken ``X``iin dağılımı bir Γ(αi, β) olursa; o halde
\sum_^N X_i \sim \Gamma \left(\sum_^N \alpha_i, \beta \right) \,\!
Ancak bütün Γ(αi, β) istatistiksel bağımsız olması gerekir.
Gamma dağılımı sonsuz bölünebilirlik özelliği gösterir.
Ölçekleme
Herhangi bir ``t`` icçin ``tX`` bir Γ(``k``, ``t``θ) dağılımı goösterir; bu ifade ``θ``nın bir ölçek parametresi olduğunu gösterir.
Üstel ailesi
Gamma dağılımı iki-parametreli üstel ailesinin bir üyesidir ve doğal parametreler değerleri ve ; ve doğal istatistikleri ve olur.
Enformasyon entropisi
Enformasyon entropisi şöyle verilir:
burada ψ(``k``) bir digamma fonksiyonu olur.
Kullback-Leibler ayrılımı
`Gerçek` dağılım olan Γ(α0, β0) ile yaklaşık fonksiyon olan Γ(α, β) arasındaki yönlendirilmiş Kullback-Leibler ayrılması şu fonksiyonla verilir:
D_)\beta_0^)\psi(\alpha)+\alpha\frac
Laplace dönüşümü
Gamma dağılımının Laplace dönüşümü şudur:
F(s)=\frac.
Parametre tahmini
Maksimum olabilirlilik tahmini
The likelihood function for ``N`` iid observations is
from which we calculate the log-likelihood function
Finding the maximum with respect to by taking the derivative and setting it equal to zero yields the maximum likelihood estimate of the θ parameter:
Substituting this into the log-likelihood function gives
Finding the maximum with respect to ``k`` by taking the derivative and setting it equal to zero yields
where
is the digamma function.
There is no closed-form solution for ``k``. The function is numerically very well behaved, so if a numerical solution is desired, it can be found using, for example, Newton`s method. An initial value of ``k`` can be found either using the method of moments, or using the approximation
If we let
then ``k`` is approximately
which is within 1.5% of the correct value.Fact|date=February 2007 An explicit form for the Newton-Raphson update of this initial guess is given by Choi and Wette (1969) as the following expression:
where denotes the trigamma function (the derivative of the digamma function).
The digamma and trigamma functions can be difficult to calculate with high precision. However, approximations known to be good to several significant figures can be computed using the following approximation formulae:
\psi\left(k\right) = \begin \ln(k) - (1 + (1 - (1/10 - 1 / (21 k^2)) / k^2) / (6 k)) / (2 k), \quad k \geq 8 \\psi\left(k + 1 \right) - 1/k, \quad k < 8 \end
and
\psi`\left(k\right) = \begin (1 + (1 + (1 - (1/5 - 1 / (7 k^2)) / k^2) / (3 k)) / (2 k)) / k, \quad k \geq 8, \\psi`\left(k + 1 \right) + 1/k^2, \quad k < 8. \end
For details, see Choi and Wette (1969).
Bayes tipi minimum ortalama-kareli hata
Bilinen degerde ``k`` ve bilinmeyen degerde `, icin theta icin sonrasal olasilik yogunluk fonksiyonu ( icin standard olcek-degeistilmez oncel kullanarak) su elde edilir:
P(\theta | k, x_1, ..., x_N) \propto 1/\theta \prod_^N f(x_i;k,\theta).\,\!
Su ifade verilsin
Bunun θ entegrasyonu degiskenlerin degistirilmesi yontemi kullanilarak mumkun olur. Bunun sonucunda 1/θ ifadesinin
\int_0^ \theta^ e^\, d\theta = \int_0^ x^ e^ \, dx = y^ \Gamma(N k -m). \!
The moments can be computed by taking the ratio (``m`` by ``m`` = 0)
E(x^m) = \frac y^m, \!
which shows that the mean +/- standard deviation estimate of the posterior distribution for theta is
Gamma dagilim gosteren rassal degisken uretimi
Given the scaling property above, it is enough to generate gamma variables with ``β`` = 1 as we can later convert to any value of ``β`` with simple division.Using the fact that a Γ(1, 1) distribution is the same as an Exp(1) distribution, and noting the method of generating exponential variables, we conclude that if ``U`` is uniformly distributed on (0, 1
where ``Uk`` are all uniformly distributed on (0, 1
All that is left now is to generate a variable distributed as Γ(δ, 1) for 0 < δ < 1 and apply the "α-addition" property once more. This is the most difficult part.
We provide an algorithm without proof. It is an instance of the acceptance-rejection method:
- Let ``m`` be 1.
- Generate , and — independent uniformly distributed on (0, 1
] variables. - If , where , then go to step 4, else go to step 5.
- Let . Go to step 6.
- Let .
- If , then increment ``m`` and go to step 2.
- Assume to be the realization of
where [1] is the integral part of ``k``, and ``ξ`` has been generated using the algorithm above with δ = (the fractional part of ``k``), ``Uk`` and ``Vl`` are distributed as explained above and are all independent.
The GNU Scientific Library has robust routines for sampling many distributions including the Gamma distribution.
İlişkili dağılımlar
Specializations
- If , then ``X`` has an exponential distribution with rate parameter λ.
- If , then ``X`` is identical to χ2(``ν``), the chi-square distribution with ``ν`` degrees of freedom.
- If is an integer, the gamma distribution is an Erlang distribution and is the probability distribution of the waiting time until the -th "arrival" in a one-dimensional Poisson process with intensity 1/θ.
- If , then ``X`` has a Maxwell-Boltzmann distribution with parameter ``a``.
Diğerleri
- Eger ``X`` bir Γ(``k``, θ) dagilimi gosterirse 1/``X`` ``k`` ve θ-1
- If ``X`` and ``Y`` are independently distributed Γ(α, θ) and Γ(β, θ) respectively, then ``X`` / (``X`` + ``Y``) has a beta distribution with parameters α and β.
- If ``Xi`` are independently distributed Γ(α``i``,θ) respectively, then the vector (``X``1 / ``S``, ..., ``Xn`` / ``S``), where ``S`` = ``X``1 + ... + ``Xn``, follows a Dirichlet distribution with parameters α1, ..., α``n``.
Referanslar
- R. V. Hogg and A. T. Craig. ``Introduction to Mathematical Statistics``, 4th edition. New York: Macmillan, 1978. ``(Bak Section 3.3.)``
- MathWorld|urlname=GammaDistribution|title=Gamma distribution
- S. C. Choi and R. Wette. (1969) ``Maximum Likelihood Estimation of the Parameters of the Gamma Distribution and Their Bias``, Technometrics, 11(4) 683-69
İçsel kaynaklar
Kaynak
- Kaynak wiki|url=http://en.wikipedia.org/w/index.php?title=Gamma_distribution|tarih= |dil=İngilizce|madde=Gamma_distribution
Olasılık Dağılımları